什么是DFS序？
dfs序是指：每个节点在dfs深度优先遍历中的进出栈的时间序列。
比如有一颗普通树，它长这样：
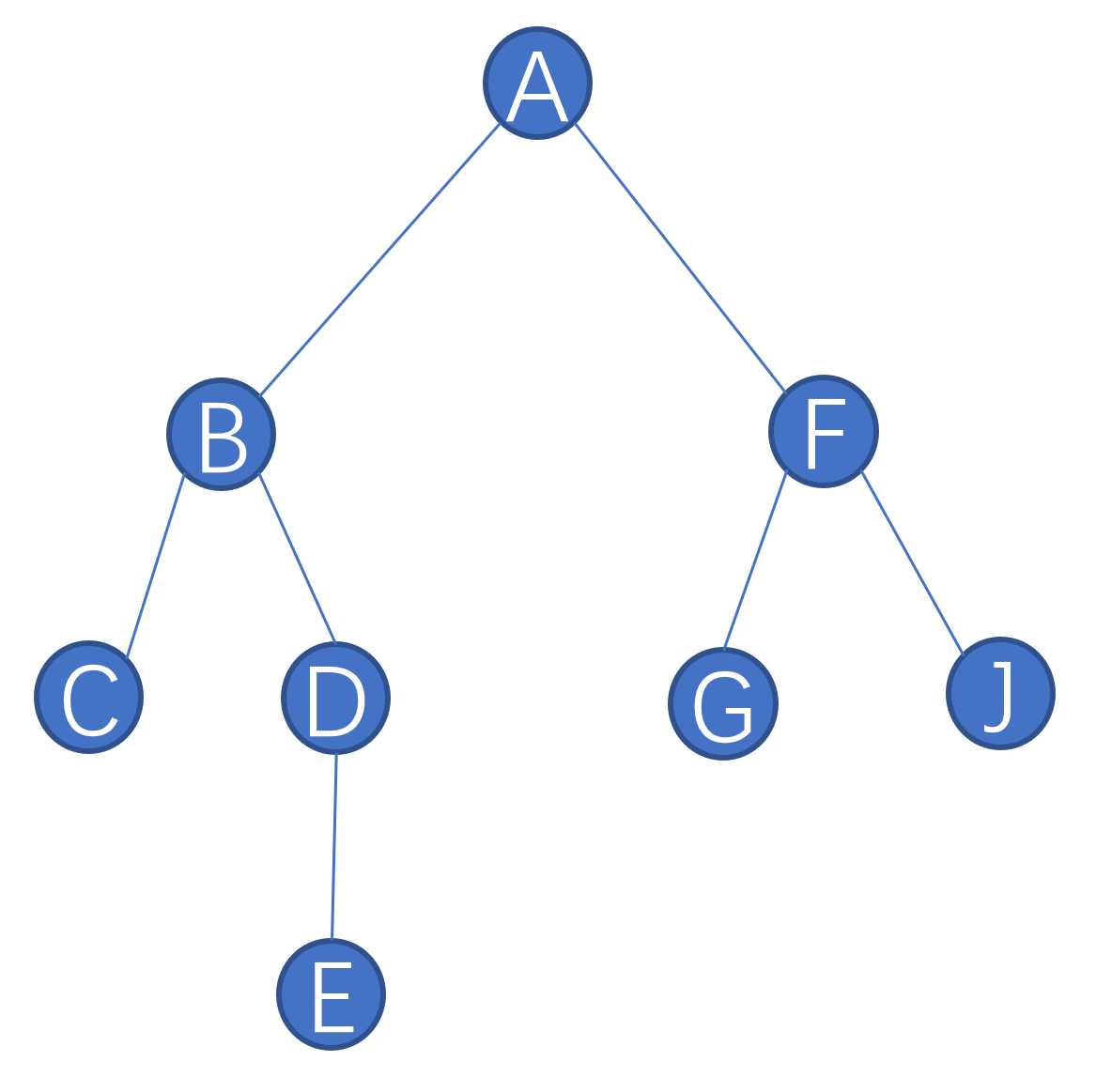
进出栈我们用一个in[i]和out[i]数组来记录，用全局变量dfn从0开始每次进栈就++，出栈就记录下来退出时候的时间，这里在Tarjan算法中也经常有，叫时间戳。
那么上图的进出栈顺序是：
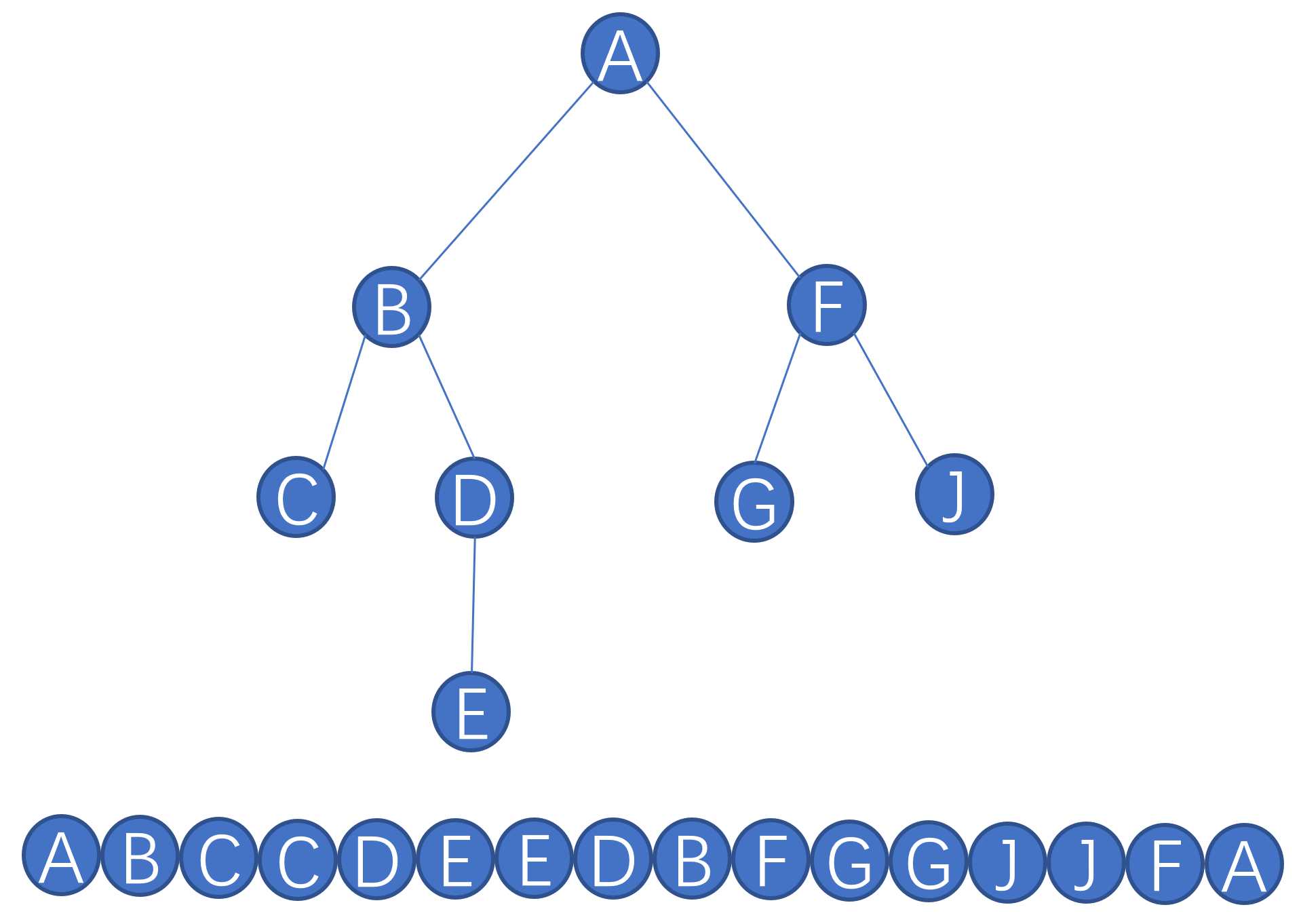
序列中第一次出现的当然就是进栈时候，第二次就是出栈的时候。出栈有两种写法，有的时候写1out[i]=++dfn，也可以写out[i]=dfn，影响不大，如果不写++的话判断的时候就会有<=这样的，因为时间戳肯定有相等的时候。
有什么用处？
1) O(1)时间判断子树
- 可以用$O(1)$的时间判断点
v是否是u的子树下的一个结点，只需要用二者的进出栈值判断：
inline bool isSubTree(int u,int v)
{
return in[u]<=in[v] && out[v]<=out[u];
}
2) 判断是否是链
- 那么如果判断一系列点是否是一条链的话，可以先按照深度排序（从小到大，也就是从父到子），然后两两比较即可。
inline bool cmp(int a,int b)
{
return dep[a]<dep[b];
}
inline bool isSubTree(int u,int v)
{
return in[u]<=in[v] && out[v]<=out[u];
}
inline bool isLink(vector<int> p)
{
sort(p.begin(),p.end(),cmp);
for (int i=1;i<p.size();i++)
if (!isSubTree(p[i-1],p[i])) return 0;//如果有不满足，那就不可以
return 1;
}
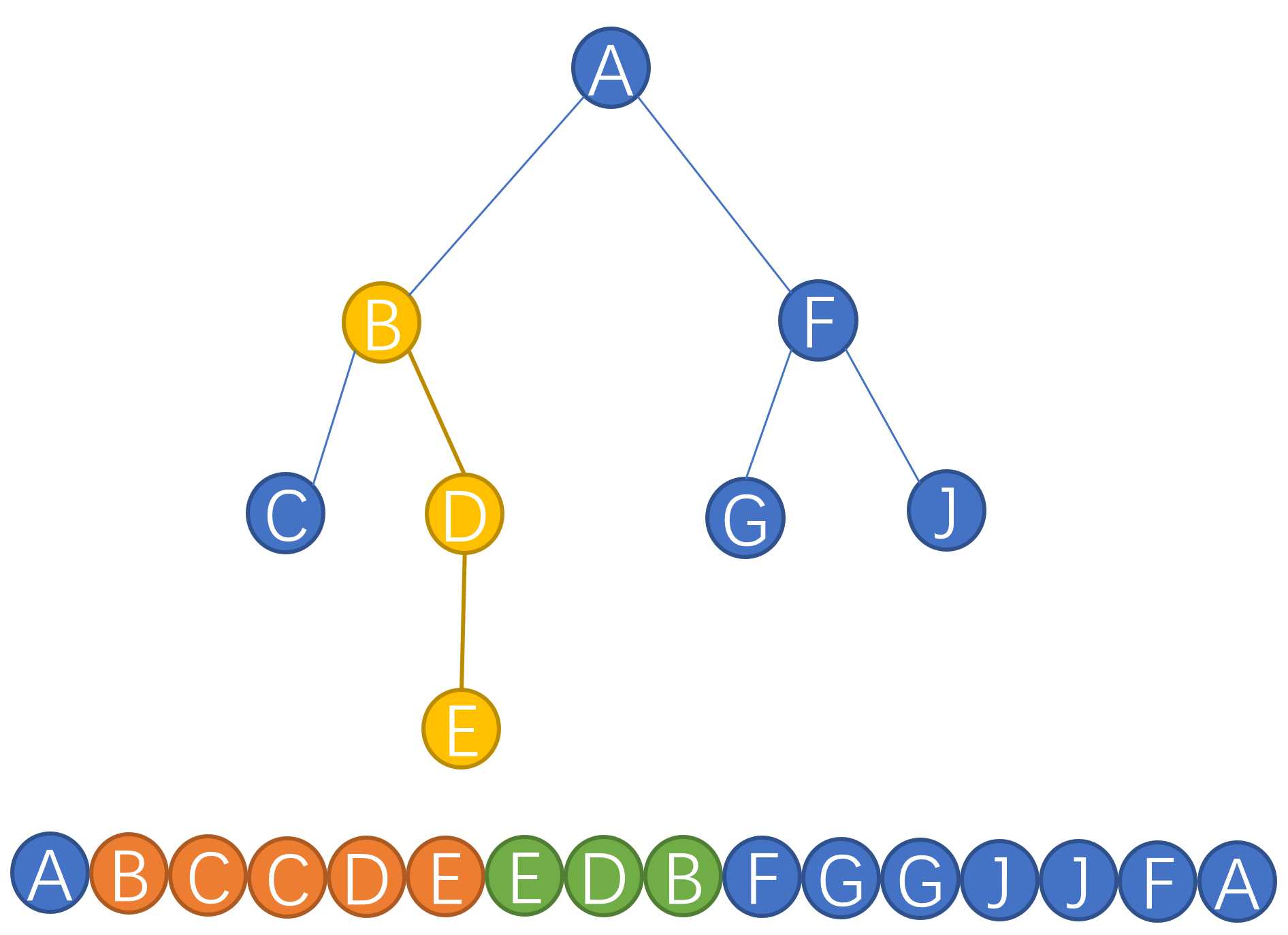
例如，我们可以看B以及B的子树：
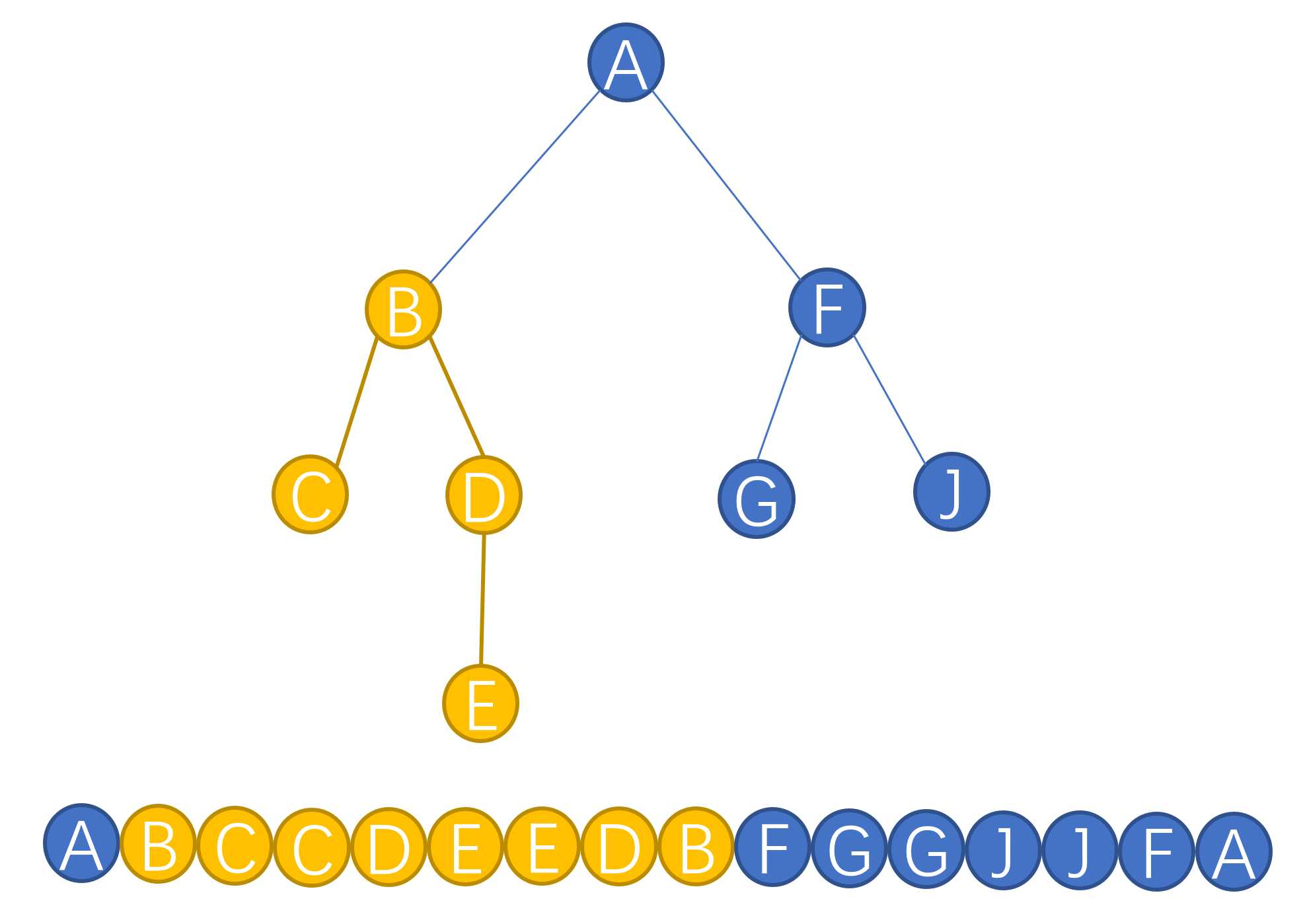
可以看出C,D,E都在B的子树下，序列也在B的入栈之后出栈之前。
3) 多个结点的LCA
- 对于多个结点的lca可以只需要求DFS序最大和最小的两个点的lca即可，也就是$LCA(x_1,x_2,\cdots ,x_k)=LCA(x_A,x_B)$，$x_A,x_B$是这$k$个点中的DFS序最大的和最小的两个点。
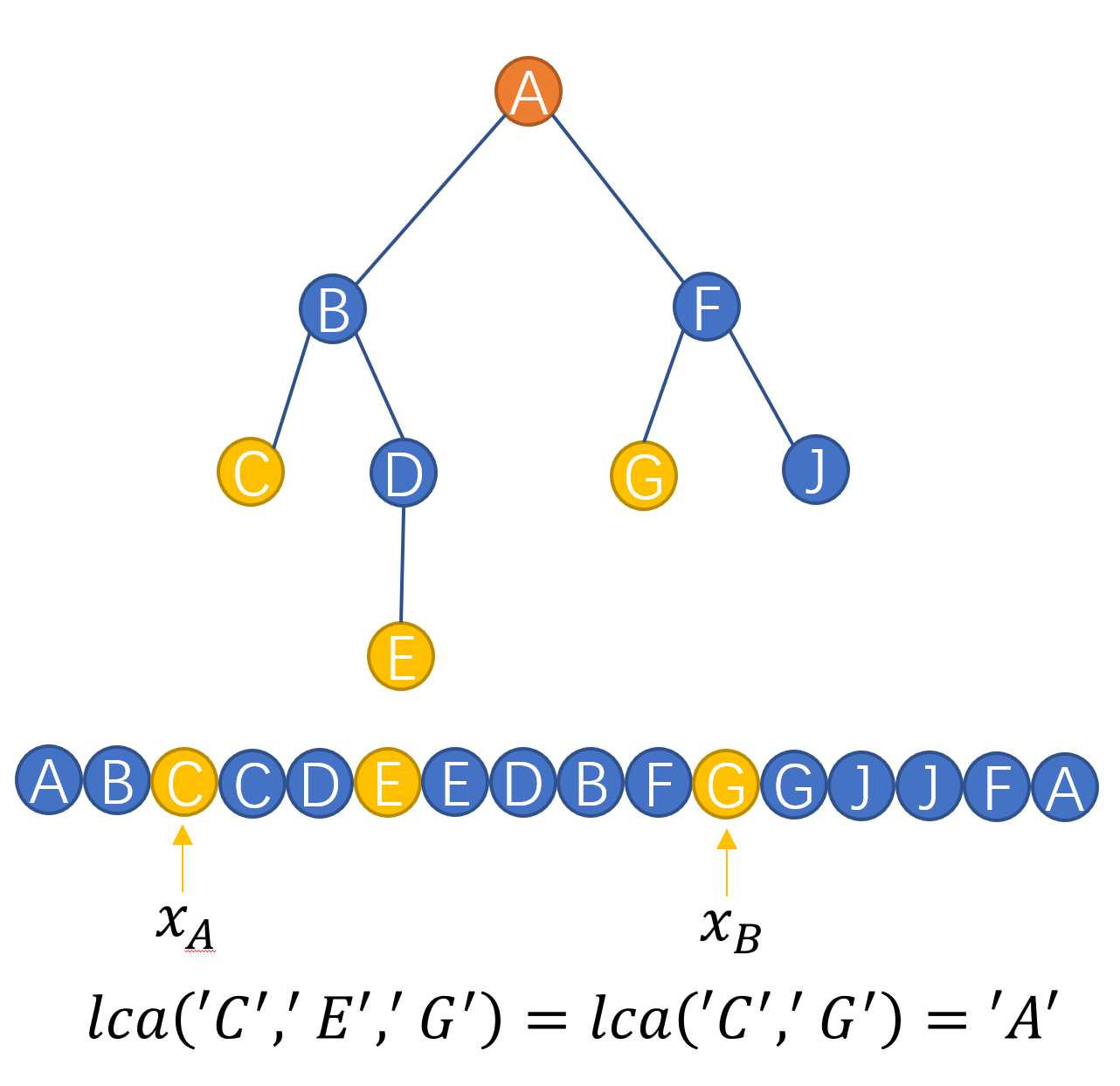
4) 求子树权值之和
在Loj有一个模板题（见下方链接），给你一颗树，单点修改权值，求某点及子树的权值之和。
我们已知一个点u的子树范围是$[in_u,out_u]$，所以我们可以转化为区间查询，查询$[in_u,out_u]$之和，那么单点修改呢？只需要修改$in_u$即可，其实$out_u$也是可以的，都是代表的u这个点。
有哪些性质？
1) 任意子树都是连续的，假如上图B的子树：$BCCDEEDB$。
2) 任意点对$(u,v)$之间的路径，可以分为两种情况：
- 无拐点。
Lca(u,v)为u,v其中一个。
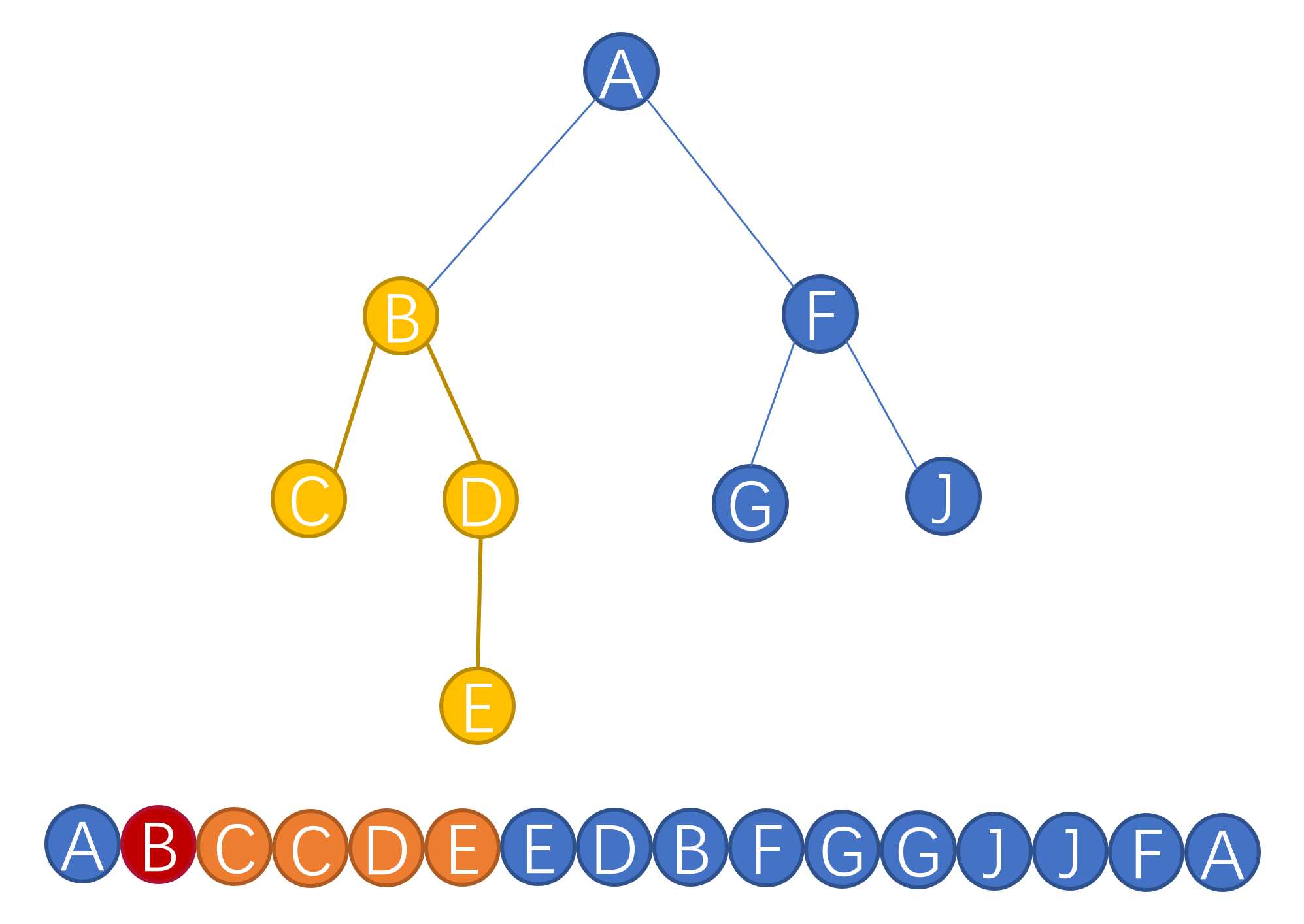
例如$BE$之间的路径就是$BCCDE$或者$EDB$。
- 有拐点。
Lca(u,v)==G而G不是u,v其中一个。
例如$CE$之间的距离，那么在$CDE$的基础上，还需要加Lca的点 $B$
利用这些性质，可以利用DFS序列完成子树操作和路径操作，同时也有可能将莫队算法应用到树上从而得到树上莫队。
第一次学习是在cf805div3:Codeforces Round #805 (Div. 3)（A~G） - CarryNotKarry
有哪些题目？
- 牛客多校3的A题
2022牛客多校·第三场（J.01BFS，H.SAM+线段树） - CarryNotKarry -
DFS序模板题，单点修改+求子树权值
LOJ#144.DFS序1
参考知识:DFS（图论） - OI Wiki (oi-wiki.org)
文章评论