COMPFEST 14 - Preliminary M. Moving Both Hands

题目链接：M. Moving Both Hands

题意

给你一个$n$点$m$边的带权有向图，一开始双手放在点$1$以及其他点，每次可以移动一只手，花费是边权，求两只手到一个点的最短时间。一共有$n-1$次询问，分别是点$1$到其他$n-1$个点的最小花费。

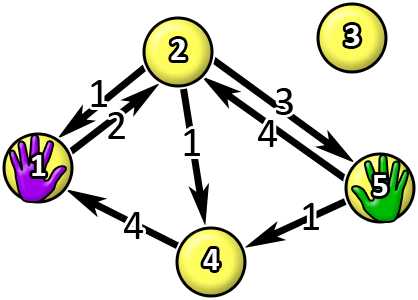
最短时间是：1->2->4 ｜ 4<-5

思路

一般这样两边同时移动的，我们可以考虑“分层图”，“反向边”，以前做过类似的题。

首先思考一个，如果是下面这条链：

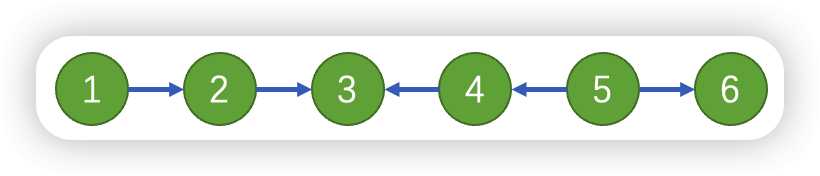
那么假设现在两只手在$1,5$上面，现在需要同时移到$3$是最佳答案，我可以看作从$1$开始可以走正向的边，可以走反向的，但是只要一旦走，那么就只能走反向的了（没有回头路）。

也就可以走$1\rightarrow 2\rightarrow 3\Rightarrow 4\Rightarrow 5$,其中$\rightarrow$是正向的，$\Rightarrow$是走反向的。也就是这种方法不可以走到$6$。

那么我可以这么思考，分层，下面再建一模一样的图，不过下面的图是反向边，也就是如下：

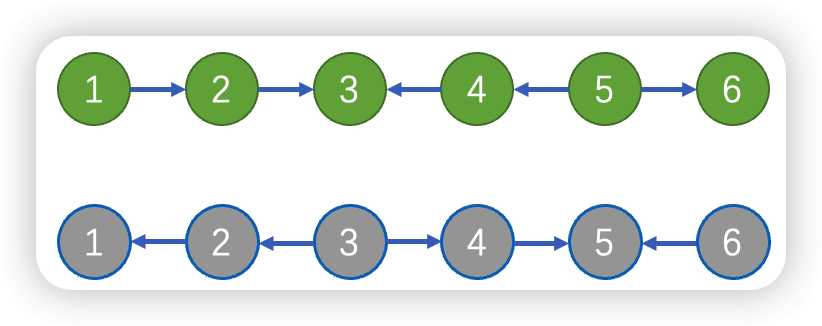
那么我下面的图是为什么反向呢？因为这时候一旦在分层图里面走就相当于可以逆向，这时候原来另一只手的$3\Leftarrow 4\Leftarrow 5$，变成了新图的$3^\prime \rightarrow 4^\prime\rightarrow 5^\prime$。

那么如何联系两层图呢？之前说的只要反向走就只能反向走了，不能回头，那么这时候我只需要对于每个点对其进行一条边权为$0$的边，可以让上面的点选择是否下去即可，这个时候可以进入，但是后面没有边可以上去，也就是这样

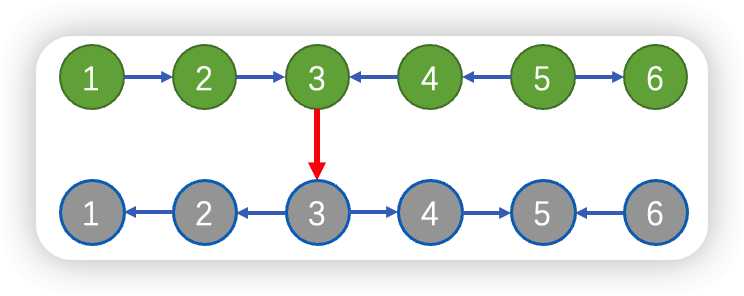
其他边权为0的边省略未画

那么这时候的路径就是：

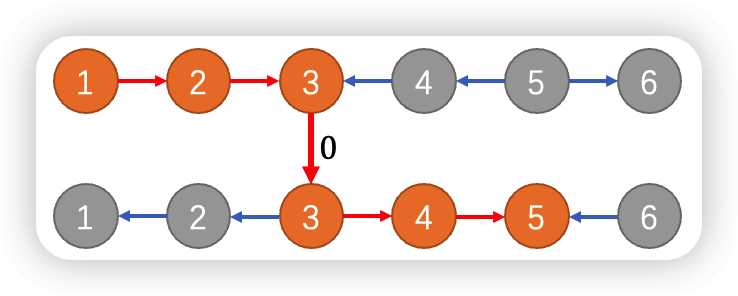
原来的路径就变成这个样子了

所以只要对于起点$1$跑一遍单源最短路Dijkstra，分层图的点就是上面的点u+n即可。

代码

inline void Case_Test()
{
    cin>>n>>m;
    for (int i=1;i<=m;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
        add(v+n,u+n,w);
    }
    for (int i=1;i<=n;i++)
        add(i,i+n,0);
    auto Dij = [&](int s)
    {
        vector<int> dis(2*n+1,inf*inf);
        priority_queue<PII> q;
        dis[s] = 0;
        q.push({0,s});
        while (!q.empty())
        {
            int x = q.top().second;
            q.pop();
            if (vis[x]) continue;
            vis[x] = 1;
            for (int i=head[x];i;i=edge[i].next)
            {
                int y = edge[i].to, w = edge[i].w;
                if (dis[y]>dis[x]+w)
                {
                    dis[y] = dis[x]+w;
                    q.push({-dis[y],y});
                }
            }
        }
        return dis;
    };
    vector<int> d = Dij(1);
    for (int i=2;i<=n;i++)
        cout<< (Min(d[i],d[i+n])>=inf*inf?-1:Min(d[i],d[i+n]))<<" ";
}