简介

二分图又称作二部图，是图论中的一种特殊模型。
最大匹配数 = 最小点覆盖 = 总点数- 最大独立集 = 总点数- 最小路径点覆盖
比如下图：

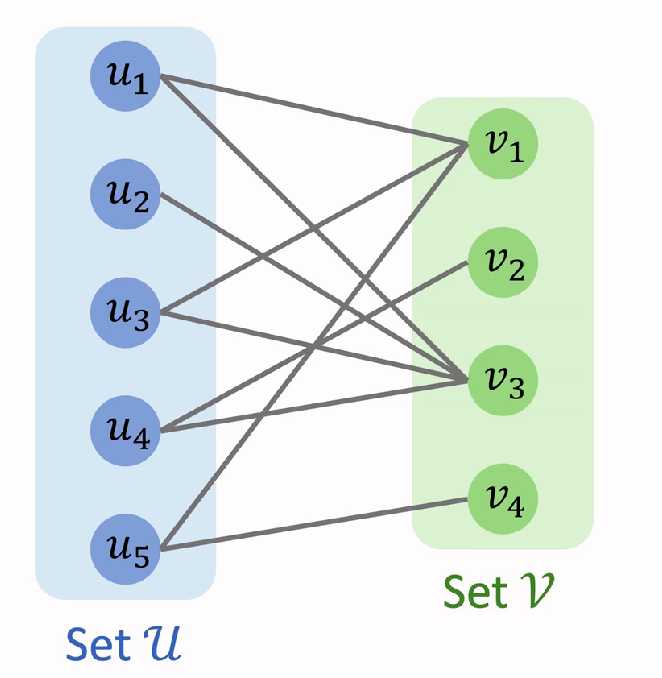
二分图匹配的话我们可以用到——匈牙利算法，二分图判定的话我们可以直接用BFS，我看有些图是DFS也是一样的道理，就是判断邻边是否颜色相同（重点）

思路

1）我们首先定一个起点，将起点加入队列deque里面，每次bfs取出来顶端的

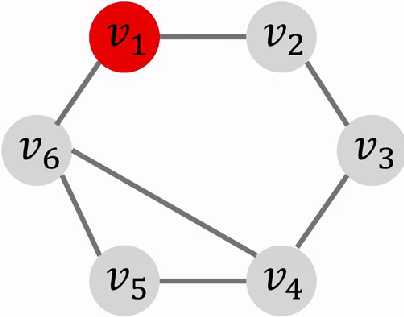
2）然后对其的所有邻边进行染色（染不同的色）
i）情况一：相邻的边没有被染色
那么也就是还没有进入过队列，那么这个时候边染成不同的色，边将其压入队列尾部

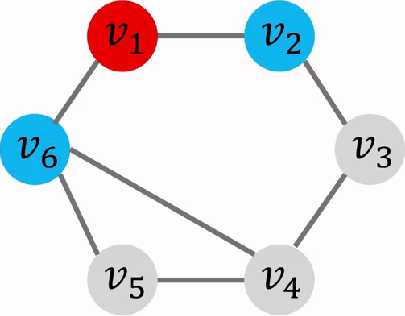
此时队列情况：一开始的$v1$已经出队列，$v2$与$v6$压入队尾
ii）情况二：相邻的边已经被染色

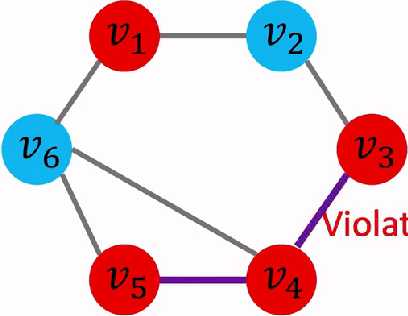
将邻边染色的时候发现邻边已经被染色，那么就判断是否是同样的颜色，如果是，那么就发生冲突，不是二分图；如果不是，则继续BFS
PS：其他例子

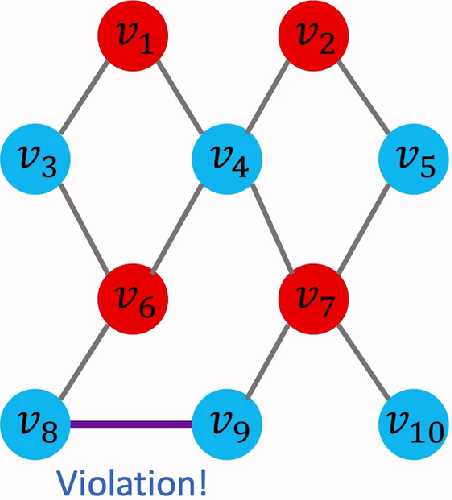
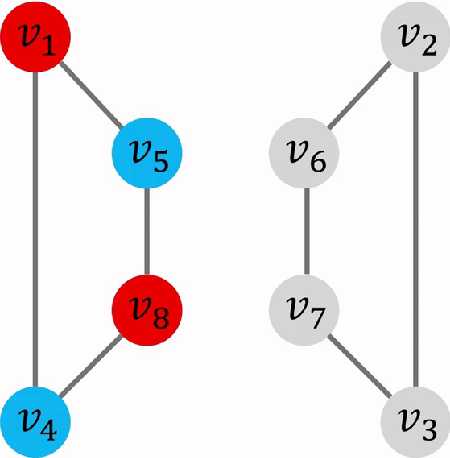
3）如果碰到未完全遍历完，那么就继续上述方法，如果有多个二分图，那么也是二分图的，因为我们同样可以做成两个集合，如下图：

代码

二分图判定

inline bool check()
{
    deque<int> q;
    q.push_front(1);vis[1]=1;color[1]=1;
    while (!q.empty())
    {
        x=q.front();q.pop_front();
        for (int i=head[x];i;i=edge[i].next)
        {
            int y=edge[i].to;
            if (!vis[y]) 
            {
                vis[y]=1;//标记已经染色过，实际上直接判断color也可
                q.push_back(y);//压入队尾
                color[y]=color[x]==1?2:1;//我用1,2代表不同的颜色
            }
            else if (color[y]==color[x]) return false;//如果冲突了，那么就不是二分图
        }
    }
    return true;
}

二分图最大匹配（匈牙利算法）

题目链接：二分图最大匹配-洛谷P3386

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 1010;
struct Edge{int to,next;}edge[1000100];
int head[N],cnt,match[N],n,ans,x,y,m,e;
bool chw[N];
inline void add(int x,int to)
{
    edge[++cnt].to=to;
    edge[cnt].next=head[x];
    head[x]=cnt;
}
inline bool Hdfs(int x)
{
  for (int i=head[x];i;i=edge[i].next)
    {
      int y=edge[i].to;
      if (chw[y])
    {
        chw[y]=false;
      if (!match[y] || Hdfs(match[y]))
        {
          match[y]=x;
          return 1;
        }
    }
    }
  return 0;
}
int main()
{
  scanf("%d%d%d",&n,&m,&e);
  for (int i=1;i<=e;i++)
    {
      scanf("%d%d",&x,&y);
        if (x>n||y>m) continue;
      add(x,y);
    }
  for (int i=1;i<=n;i++)
    {
      memset(chw,1,sizeof(chw));
      if (Hdfs(i)) ans++;
    }
  printf("%d",ans);
}