POJ3304 Segments （叉积判断直线与线段关系）

题意

题目链接：
AcWing 2984.线段
POJ寄了

在二维平面内有 $n$ 条线段，请你编写一个程序，判断是否存在一条直线满足将这 $n$ 条线段投影到该直线上后，所有的投影线段至少具有一个公共点。

数据范围
$1≤T≤100,
1≤n≤100,
−10^9≤x1,y1,x2,y2≤10^9$

思路

先来看看题意，题目给出若干线段，需要找到一条线段，线段的投影在直线上需要有交点，也就是下图三条线段，需要找一条直线往其做投影，需要找到至少一个公共点。

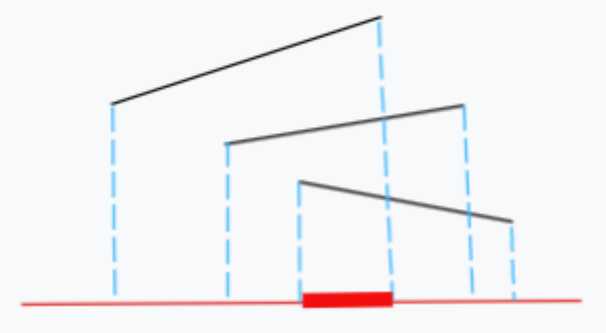
那么如何来找到这样的直线呢？这样按照题意十分复杂，所以需要转换题意，我们试着对这条直线做垂线，也就是与线段投影的垂线平行的线。

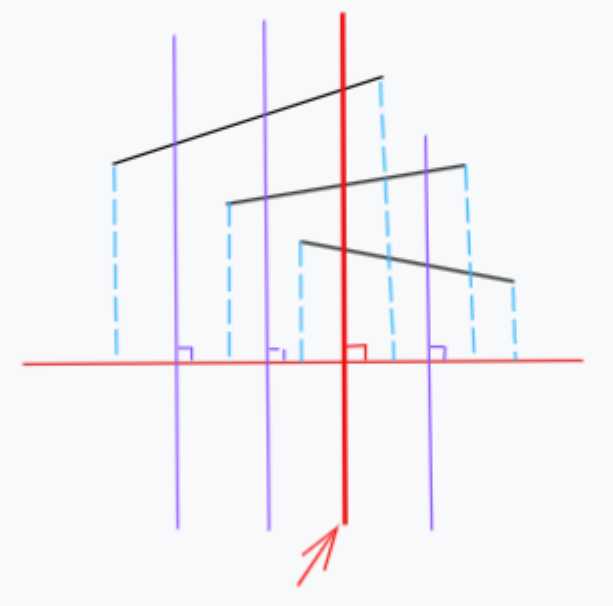
可以把问题转化为，找到一根直线，可以穿过所有的线段，因为这条直线与线段都会有一个交点，这个交点在题目要求的直线上会聚集在一个点，满足题意。

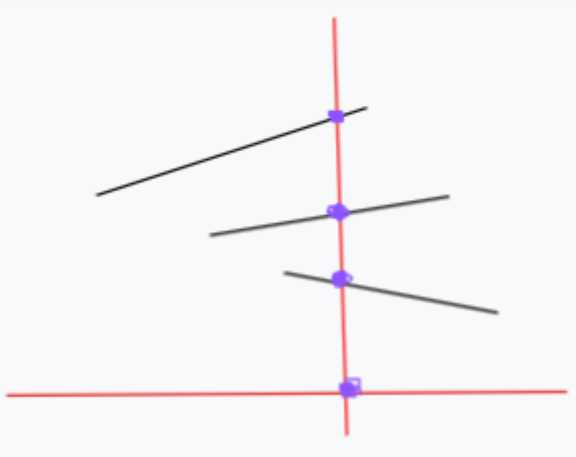
那么现在的问题是如何能够找到穿过这$n$条线段的直线？先在最外面找一个点，往左边倾斜，可以看出一定会有一个点卡住不能再往右。

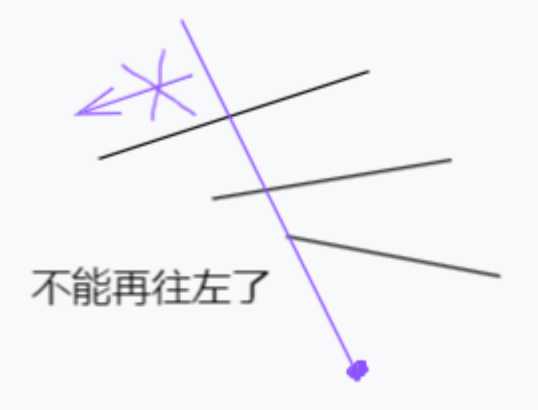
然后再固定不能左的那个点往右边找边界。

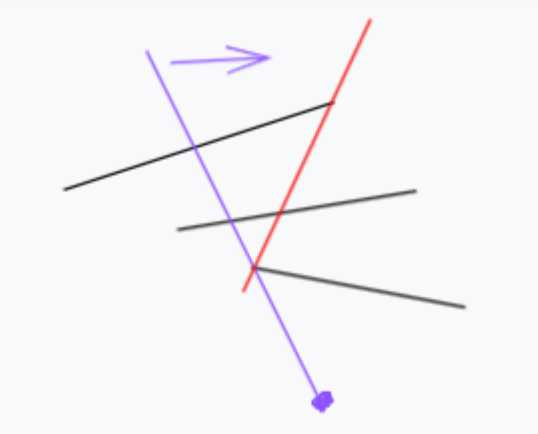
这样就找到了那条能够穿过所有线段的直线了。

那么现在可以看出，实际上就是枚举$n$条线段的$2n$个端点，选取这两条组成一条直线再枚举$n$条直线进行check()，判断找到的这两个端点组成的直线是否能穿过所有的线段？

那么问题来了，一条直线是否能够穿过线段怎么判断呢？

前置知识：如何判断点在直线的左侧还是右侧。
在这篇文章已经讲过POJ2318 Toys（计算几何） - CarryNotKarry，只需要形成两条向量进行叉积判断，也就是用到右手法则判断sin的大小即可。

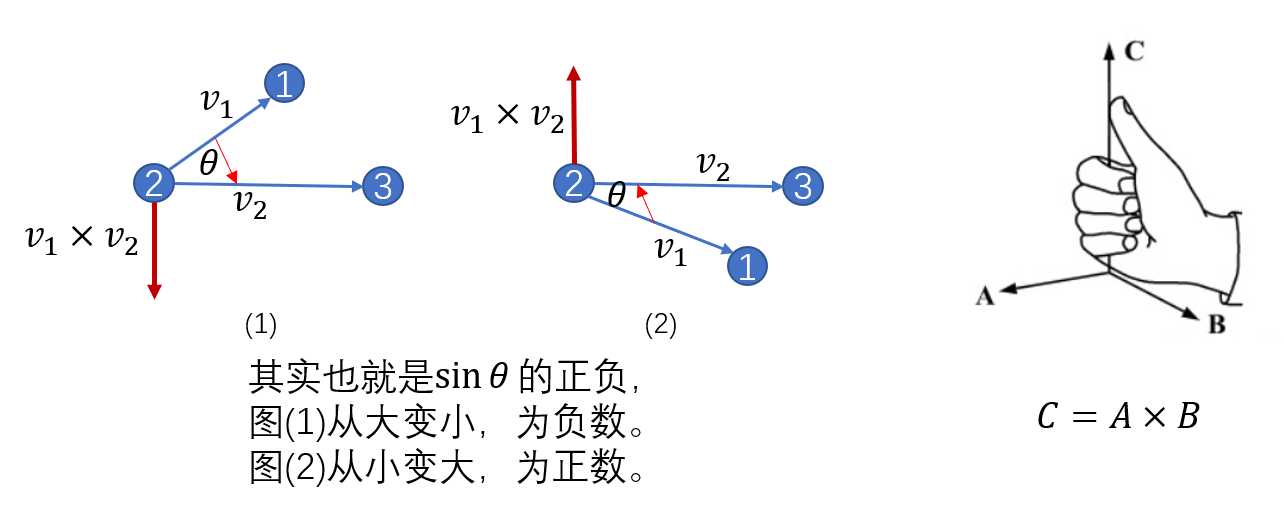
那么一条线段与直线的关系呢？——两个端点都在直线的同一侧，也就是二者的cross叉积都大于0.

inline double cross(Point A,Point B)
{
    return A.x*B.y-A.y*B.x;
}
inline int relation(Point A,Point B,Point C)
{
    int c = sgn(cross(B-A,C-A));
    if (c<0) return 1;
    if (c>0) return -1;
    return 0;
}

然后比较第i条线段的两个端点a[i],b[i],用if (relation(p[x],p[y],a[i])*relation(p[x],p[y],b[i])>0)即可判断，因为在同一侧符号相同。

为了方便我重载了一下-号。

struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y):x(_x),y(_y){}
    Point operator - (const Point &p){
        return Point(x-p.x,y-p.y);
    }
}a[N],b[N],p[N];

所以总的来看就是枚举两个端点，这两点组成一条直线，枚举所有的线段都判断是否在其的同一侧。

代码

const double eps = 1e-8;
struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y):x(_x),y(_y){}
    Point operator - (const Point &p){
        return Point(x-p.x,y-p.y);
    }
}a[N],b[N],p[N];
int n,cnt;
inline int sgn(double x)
{
    if (fabs(x)<eps) return 0;
    if (x<0) return -1;
    return 1;
}
inline int cmp(double x,double y)
{
    if (fabs(x-y)<eps) return 0;
    if (x<y) return -1;
    return 1;
}
inline double cross(Point A,Point B)
{
    return A.x*B.y-A.y*B.x;
}
inline int relation(Point A,Point B,Point C)
{
    int c = sgn(cross(B-A,C-A));
    if (c<0) return 1;
    if (c>0) return -1;
    return 0;
}
inline bool check(int x,int y)
{
    for (int i=1;i<=n;i++)
        if (relation(p[x],p[y],a[i])*relation(p[x],p[y],b[i])>0) return false;
    return true;
}
inline void Case_Test()
{
    cin>>n;
    cnt = 0;
    for (int i=1;i<=n;i++)
    {
        cin>>a[i].x>>a[i].y>>b[i].x>>b[i].y;
        p[cnt++] = a[i];p[cnt++] = b[i];
    }
    for (int i=0;i<cnt;i++)
        for (int j=i+1;j<cnt;j++)
        {
            if (cmp(p[i].x,p[j].x)==0&&cmp(p[i].y,p[j].y)==0) continue;
            if (check(i,j)) 
            {
                cout<<"Yes!"<<endl;
                return;
            }
        }
    cout<<"No!"<<endl;
}

感觉全网没有写的比我的还清楚的题解了哈哈哈。