题意
题目链接:Mayor's posters - POJ 2528 - Virtual Judge (vjudge.net)
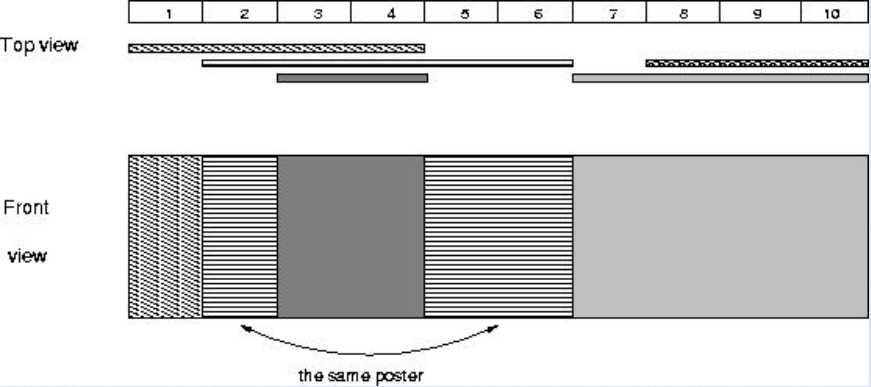
有$T$组数据,每次有$n$个区间,第$i$个区间将会把$[l_i,r_i]$染成$i$颜色,最后从上往下看有多少种不同的颜色?
数据范围
$1\leq n\leq 10000$
$1\leq l_i\leq r_i\leq 10^7$
思路
区间太大,肯定不能用这么大的数组($O(nlogn)$),又注意到$n$比较小,所以要用到离散化。
比如这个样例:
7 11
7 8
10 11
那么我可以排序加去重得到$\lbrace 7,8,10,11\rbrace$,这样四个数在我离散化后面就变成了$\lbrace 1,2,3,4\rbrace$,我对$[7,8]$染成$2$号颜色,在我这个线段树中就变成了将$[1,2]$染成$2$号颜色,这就是离散化。
那么这样就够了吗?——不够!
就如上面的三个区间而言,本来应该是三种颜色的(第一种颜色在$9$),但是我们离散化把$9$没有离散化成3,所以我们要进行一个填空的操作:
我们排序去重发现是$\lbrace 7,8,10,11\rbrace$之后,我们扫一遍判断,如果中间有不连续的,那么就手动填一个进去,比如$7,8$之间是连续的,不用管;$8,10$之间不连续,所以需要填一个任意的进去,这里我填$9$,这样就变成了$\lbrace 7,8,9,10,11\rbrace$,离散化的时候$10$对应的$4$,这样下来就没有覆盖$9$了,也没有把$9$遗忘掉。
其实不填也可以,我只是让不连续的多$+1$即可,比如本来应该$10$此时应该是$3$,但是我让他$+1$变成$4$。
for (int i=1;i<=m;i++)
{
a[i].x = read();a[i].y = read();
b[++cnt] = a[i].x;
b[++cnt] = a[i].y;//离散化
vis[i] = 0;
}
sort(b+1,b+cnt+1);//排序
int num=0;
mp[b[1]] = ++num;
for (int i=2;i<=cnt;i++)
{
if(b[i]-b[i-1]==1)
mp[b[i]]=++num;
else if(b[i]==b[i-1])//重复,去重
continue;
else
{
num++;//多+1
mp[b[i]]=++num;
}
}
然后就是线段树的内容了。染色的话实际上就是区间赋值,把普通的+=改为=即可。这里我发现只需要tag就好,并且没有pushup,用一个全局变量vis[]来判断颜色是否出现过,最后递归到有tag的时候就好。
注意这里的tag如果当前结点有(不为0)的话,那么就不用下去了,直接判断返回即可,因为下面必定一样,不一样的话说明这个结点一定经过过,那么也就说明这个tag一定下放过,矛盾了,所以就可以直接判断返回。
线段树代码如下:
struct Segment_Tree
{
int tag[N<<2],lc[N<<2],rc[N<<2];
#define lson (o<<1)
#define rson (o<<1|1)
#define mid ((l+r)>>1)
inline void build(int o,int l,int r)
{
lc[o]=l;rc[o]=r;tag[o]=0;
if (l==r) return;
build(lson,l,mid);build(rson,mid+1,r);
}//tag一开始全部为0.
inline void pushdown(int o)
{
if (tag[o])
{
tag[lson] = tag[o];
tag[rson] = tag[o];
tag[o] = 0;
}
}//下放
inline void update(int o,int ql,int qr,int k)
{
int l = lc[o], r = rc[o];
if (ql<=l&&r<=qr)
{
tag[o] = k;
return;
}//整个结点都在里面
pushdown(o);
if (ql<=mid) update(lson,ql,qr,k);
if (qr>mid) update(rson,ql,qr,k);
}
inline void query(int o)
{
int l = lc[o], r = rc[o];
if (tag[o])
{
if (!vis[tag[o]]) vis[tag[o]] = 1, ans++;
return;
}
if (l==r) return;
//一定要有这个判断,不然会tle,我一直找这个bug
//不是所有的结点都有tag[o],所以这里直接返回就好(到达叶子节点)
pushdown(o);
query(lson);query(rson);
}
}tree;
代码
完整代码
struct Segment_Tree
{
int tag[N<<2],lc[N<<2],rc[N<<2];
#define lson (o<<1)
#define rson (o<<1|1)
#define mid ((l+r)>>1)
inline void build(int o,int l,int r)
{
lc[o]=l;rc[o]=r;tag[o]=0;
if (l==r) return;
build(lson,l,mid);build(rson,mid+1,r);
}
inline void pushdown(int o)
{
if (tag[o])
{
tag[lson] = tag[o];
tag[rson] = tag[o];
tag[o] = 0;
}
}
inline void update(int o,int ql,int qr,int k)
{
int l = lc[o], r = rc[o];
if (ql<=l&&r<=qr)
{
tag[o] = k;
return;
}
pushdown(o);
if (ql<=mid) update(lson,ql,qr,k);
if (qr>mid) update(rson,ql,qr,k);
}
inline void query(int o)
{
int l = lc[o], r = rc[o];
if (tag[o])
{
if (!vis[tag[o]]) vis[tag[o]] = 1, ans++;
return;
}
//if (tag[o]&&!vis[tag[o]]) vis[tag[o]] = 1, ans++;
if (l==r) return;
pushdown(o);
query(lson);query(rson);
}
}tree;
struct node
{
int x,y;
}a[N];
int b[N];
map<int,int> mp;
inline void Case_Test()
{
m = read();
mp.clear();
cnt = 0;
ans = 0;
for (int i=1;i<=m;i++)
{
a[i].x = read();a[i].y = read();
b[++cnt] = a[i].x;
b[++cnt] = a[i].y;
vis[i] = 0;
}
sort(b+1,b+cnt+1);
int num=0;
mp[b[1]] = ++num;
for (int i=2;i<=cnt;i++)
{
if(b[i]-b[i-1]==1)
mp[b[i]]=++num;
else if(b[i]==b[i-1])
continue;
else
{
num++;
mp[b[i]]=++num;
}
}
tree.build(1,1,num);
for (int i=1;i<=m;i++)
{
int x,y;
x = mp[a[i].x];
y = mp[a[i].y];
tree.update(1,x,y,i);
}
tree.query(1);
writeln(ans);
}
