题意
给定长度为 N 的数列 A,以及 M 条指令,每条指令可能是以下两种之一:
1. 1 x y,查询区间$[x,y]$种的最大连续子段和,即
$$
\max {x \leq l \leq r \leq y}\lbrace \sum{i=l}^{r} A[i] \rbrace
$$
2 x y,把$A[x]$改成$y$
对于每一个查询指令,输出一个整数表示答案。
题目来源于AcWing245,245. 你能回答这些问题吗 - AcWing题库
思路
以前我的线段树都是封装的,但是对于这样的询问需要返回不止一个值,例如这里在查询操作需要返回的是当前node结点,所以我之类还是不封装,写一个struct node类。
struct node
{
int l,r,tmax,lmax,rmax,sum;
}tr[N<<2];
tmax表示的是当前结点的最大子段和。lmax表示的是当前节点从左端点往右的最大子段和rmax表示的是当前节点从右端点往左的最大子段和sum表示的是当前节点的所有值的和
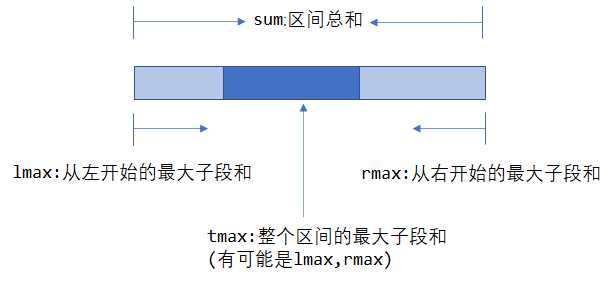
为什么需要设置lmax和rmax以及sum,因为我们在合并区间的时候,可能最大子段和在跨区间的部分,具体见pushup,好吧这就写哈哈!
这里为了简便写两个pushup,主要看另外一个,这个跟平时不一样,因为我这里传入的比较多,又是用的是node类,所以我这里传入的根节点,左右儿子结点,并且pushup里面是引用,可以修改。
对于维护四个值:
1. 维护sum,那当然是左右两个sum相加
- 维护
lmax,那自然是左儿子的lmax与横跨两个结点的最大子段和来看,也就是左儿子的整段sum加上右儿子的lmax,这样就维护了当前根节点区间的`lmax

- 维护
rmax,与上述一样,用右儿子的rmax与跨区间的比较,也就是右儿子的sum加上左儿子的rmax -
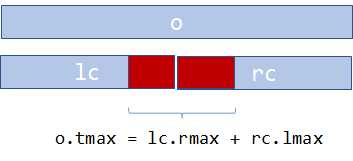
维护当前结点的最大子段和
tmax,有三种情况:左儿子的最大子段和tmax,右儿子的最大子段和tmax,横跨左右儿子的最大子段和左儿子的rmax和右儿子的lmax
inline void pushup(node &o,node &lc,node &rc)
{
o.sum = lc.sum + rc.sum;
o.lmax = Max(lc.lmax,lc.sum+rc.lmax);
o.rmax = Max(rc.rmax,rc.sum+lc.rmax);
o.tmax = Max( Max(lc.tmax,rc.tmax) , lc.rmax+rc.lmax );
}
inline void pushup(int o)
{
pushup(tr[o],tr[lson],tr[rson]);
}
建树的话还是一样,一开始叶子结点的tmax,lmax,rmax,sum都等于a[l]。
inline void build(int o,int l,int r)
{
tr[o].l = l; tr[o].r = r;
if (l==r)
{
tr[o].tmax = tr[o].lmax = tr[o].rmax = tr[o].sum = a[l];
return;
}
build(lson,l,mid);build(rson,mid+1,r);
pushup(o);
}
然后来看修改,如果到叶子结点,那么需要将上述四个值都改为k,单点修改需要拿x去与mid比较。最后pushup更新。
inline void modify(int o,int x,int k)
{
if (tr[o].l == tr[o].r) {tr[o] = {x,x,k,k,k,k};return;}
if (x<=mid) modify(lson,x,k);
else modify(rson,x,k);
pushup(o);//递归更新
}
最后是查询,因为这里传入的变量比较多,所以就不再像以前那样写int query(...)了,而是返回一个node结点。
这里有两种写法,可以像y总那样分为三种情况,在左边,在右边,都在。也可以像我这样首先设置并且初始化两个结点,然后进行合并。
如果整段都在查询区间里面,那么就不需要往下了,直接return 当前结点。
inline node query(int o,int l,int r)
{
if (l<=tr[o].l && tr[o].r<=r) return tr[o];
node left={0,0,-inf,-inf,-inf,-inf},right={0,0,-inf,-inf,-inf,-inf},res;
if (l<=mid) left = query(lson,l,r);
if (r>mid) right = query(rson,l,r);
pushup(res,left,right);
return res;
}
也可以像y总那样
Node query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else
{
auto left = query(u << 1, l, r);
auto right = query(u << 1 | 1, l, r);
Node res;
pushup(res, left, right);
return res;
}
}
}
作者:yxc
所以线段树大致这样就完成了,单点修改也掌握了许多。
代码
const int N = 5e5+7;
int a[N];
#define lson (o<<1)
#define rson (o<<1|1)
#define mid ((tr[o].l+tr[o].r)>>1)
struct node
{
int l,r,tmax,lmax,rmax,sum;
}tr[N<<2];
inline void pushup(node &o,node &lc,node &rc)
{
o.sum = lc.sum + rc.sum;
o.lmax = Max(lc.lmax,lc.sum+rc.lmax);
o.rmax = Max(rc.rmax,rc.sum+lc.rmax);
o.tmax = Max( Max(lc.tmax,rc.tmax) , lc.rmax+rc.lmax );
}
inline void pushup(int o)
{
pushup(tr[o],tr[lson],tr[rson]);
}
inline void build(int o,int l,int r)
{
tr[o].l = l; tr[o].r = r;
if (l==r)
{
tr[o].tmax = tr[o].lmax = tr[o].rmax = tr[o].sum = a[l];
return;
}
build(lson,l,mid);build(rson,mid+1,r);
pushup(o);
}
inline void modify(int o,int x,int k)
{
if (tr[o].l == tr[o].r) {tr[o] = {x,x,k,k,k,k};return;}
if (x<=mid) modify(lson,x,k);
else modify(rson,x,k);
pushup(o);
}
inline node query(int o,int l,int r)
{
if (l<=tr[o].l && tr[o].r<=r) return tr[o];
node left={0,0,-inf,-inf,-inf,-inf},right={0,0,-inf,-inf,-inf,-inf},res;
if (l<=mid) left = query(lson,l,r);
if (r>mid) right = query(rson,l,r);
pushup(res,left,right);
return res;
}
#undef lson
#undef rson
#undef mid
int n,m,k,x,y;
inline void Case_Test()
{
cin>>n>>m;
for (int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--)
{
cin>>k>>x>>y;
if (k==1)
{
if (x>y) swap(x,y);
cout<<query(1,x,y).tmax<<endl;
}
else
modify(1,x,y);
}
}
