题意
题目链接:1064. 小国王 - AcWing题库
在 $n×n$ 的棋盘上放 $k$ 个国王,国王可攻击相邻的 $8$ 个格子,求使它们无法互相攻击的方案总数。
数据范围
$1≤n≤10,$
$0≤k≤n^2$
样例输入
3 2
样例输出
16
思路
这是一个状压DP,数据范围比较小,状压DP主要思想就是:state转化成二进制,每一位的0或1代表一个状态。
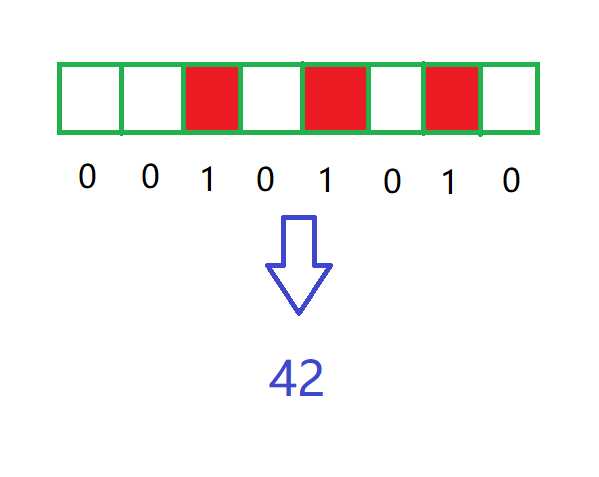
比如我们对一层$1×8$的棋盘,每一位如果放了国王,那么就是1,那么如下图的状态,我们可以用42(2+8+32)表示
先定义状态:f[i][j][s]表示一个集合,所有只摆了前i行,以及摆了j个国王,并且第i行摆放的状态是s的所有集合。
例如f[2][5][42],那么就是上图,有两层,第i层(当前)的状态是00101010,这一层摆放了3个国王,那么状态肯定是从f[1][5-3][s]转移而来,这里的s有很多种,但是在这里貌似没有...(第一行要跟第二行不冲突,且摆放两个...)好像只有10000000这种摆放一个的情况。
那么你会说,这个时候的f[2][5][42]怎么办?答案是0,为什么?因为你从f[1][2][128]转移过来,这个时候f[1][2][128]会是0.
但是如果是f[2][4][42],那么是从f[1][1][128]转移过来,显然这里也可以从f[0][0][0]转移来的,所以这个时候f[2][4][42]是1.
那么我们对于进行状态转移,对于f[i][j][s]来说,我们是摆了前i行,j个国王,当前状态是s的集合,可以从i-1行,j-count(s)个国王,状态为b的状态集合转移过来。(j-count(s)是这一行摆了count(s)个国王,那么上一个转移过来的肯定是少这么多个的)
那么状态转移之间的条件是什么?假如有两个状态a,b(分别表示i-1和i行的状态):
1)a,b内部都不能有相邻的1
2)a,b之间不能互相攻击到
· 每一位都不能同时是1,那么两个的并起来全为0,不能有1&1=1的情况。即(a&b)==0。
· 相邻也不能有,比如010和100,这两个1会有冲突,那么写一个check(a|b),(a|b)不能有两个相邻的1
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 12, M = 1 << 10, K = 110;
int n, m;
vector<int> state;
int cnt[M];
vector<int> head[M];
int f[N][K][M];
inline bool check(int state)
{
for (int i = 0; i < n; i ++ )
if ((state >> i & 1) && (state >> i + 1 & 1))
return false;
return true;
}//不能有相邻
int count(int state)
{
int res = 0;
for (int i = 0; i < n; i ++ ) res += state >> i & 1;
return res;
}//有多少1
signed main()
{
cin>>n>>m;
for (int i=0;i<1<<n;i++)
if (check(i))
{
state.push_back(i);//状态i的下标是state存放的下标
cnt[i]=count(i);
}
for (int i=0;i<state.size();i++)
for (int j=0;j<state.size();j++)
{
int a=state[i],b=state[j];
if ((a&b)==0&&check(a|b))
head[i].push_back(j);
}
f[0][0][0]=1;
for (int i = 1; i <= n ; i ++ )
for (int j = 0; j <= m; j ++ )
for (int a = 0; a < state.size(); a ++ )
for (int b : head[a])
{
int c=cnt[state[a]];
if (j >= c)
f[i][j][ state[a] ] += f[i - 1][j - c][ state[b] ];
//f[i][j][a] += f[i - 1][j - c][b];这里也能写这样,因为一一对应了
}
int ans=0;
for (int i=0;i<1<<n;i++)
ans+=f[n][m][i];//最后状态为i都是满足条件的
cout<<ans<<endl;
}
实际上最后可以不用循环找ans,直接把for循环的第一行i<=n变成i<=n+1,最后输出f[n+1][m][0]即可,其实不难想到,因为最后一个状态是0,那么把所有上一层结果都转移到了f[n][m][0]里面了
