46届ICPC上海站Steadily Growing Steam（DP）

写在前面

这是去年ICPC上海站，我们队伍获得铜尾的比赛，曹佬手撕三维DP怒秀我和郎队，现在来看，好像也没有那么难嘿嘿，可能是自己刷了一些DP题。

题意

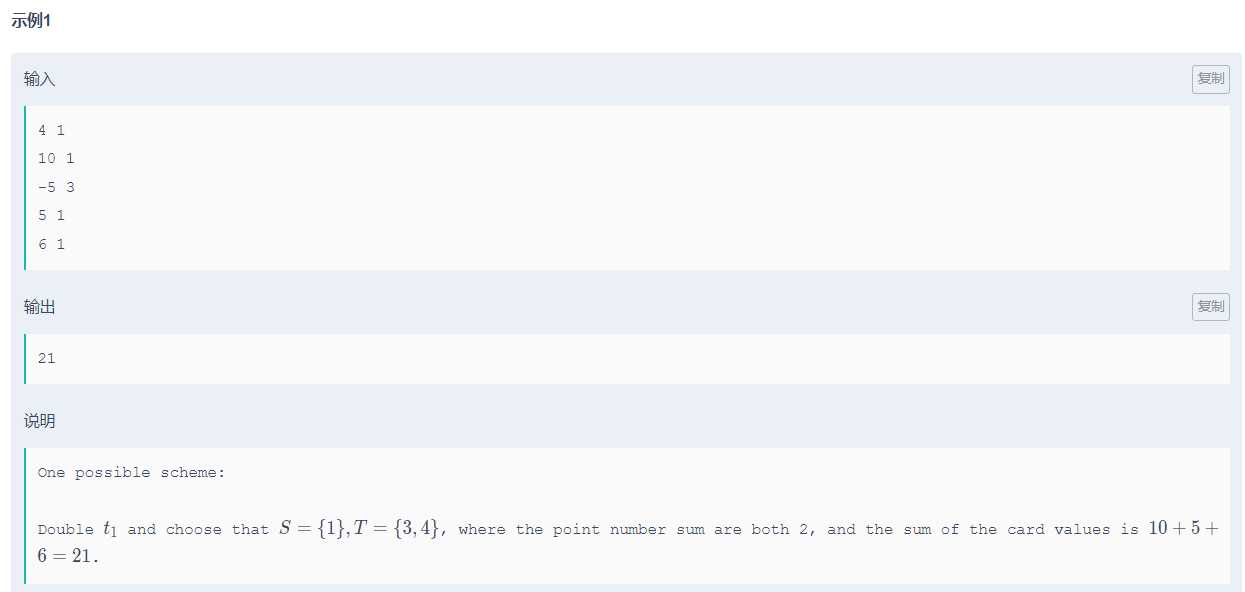
给你一个$n$个物品，每个物品有$v,t$两个属性，$v$是值，$t$是点数，现在你需要从里面取出若干份分成两堆（也就是说有的可以不选），求两堆的点数相等的时候的两堆的值的最大值。嘿嘿，没这么简单，还有一个条件，你最多有$k$次操作，可以使其中一个点数翻倍，也就是说，有可能让其翻倍之后正好两堆相同，这个时候更大，不然难以找到匹配的让其相等。

思路

其实就是背包问题吧，主要就是一个翻倍的操作，从数据范围来看，$n,k$并不大，最大才$100$，点数最多也才$13$，所以我们定义一个数组dp[i][j][k]表示前$i$个物品，已经翻倍了$j$次，两堆的“分数”达到的$k$的最大值

这里$t$最大13，$n$最大$100$，那么直接令$M=1300$，然后分成AB两堆可以理解为：如果放在A堆，那么就加，如果放在B堆，那么就减。比如一开始是$k=0$，来了一个$t=5$的，放在A堆，这个时候$k=5$，这个时候来了一个$t=3$，如果放在A堆，这个时候是加法，$k=8$，这个$8$理解为$3+5$；那么如果这个放在B堆呢？$k=5-3=2$，我们最后只需要统计$k=0$的时候，这个时候是AB两堆相等的时候。

因为有负数，所以我们需要扩大起始点，令此时的$M$为“0”，也就是本来的$(-M,M)$变为了$(0,2*M)$，很常见的技巧，然后就进行背包即可。

我们发现每次只与上一次有关联，所以我用的回滚数组，其实开三维也行，我当时是怕爆。

代码

int f[110][2630],g[110][2630];
inline void Case_Test()
{
    cin>>n>>k;
    for (int i=1;i<=n;i++) cin>>a[i]>>b[i];
    memset(f,233,sizeof(f));
    f[0][M]=0;
    for (int p=1;p<=n;p++)
    {
        memcpy(g,f,sizeof(f));
        for (int i=0;i<p&&i<=k;i++)
        {
            for (int j=0;j<2*M;j++)
            {
                if (b[p]<=j) g[i][j]=Max(g[i][j],f[i][j-b[p]]+a[p]);//不翻倍 +
                if (b[p]+j<=2*M) g[i][j]=Max(g[i][j],f[i][j+b[p]]+a[p]);//不翻倍 -
                if (b[p]*2<=j&&i>0) g[i][j]=Max(g[i][j],f[i-1][j-b[p]*2]+a[p]);//翻倍 +
                if (b[p]*2+j<=2*M&&i>0) g[i][j]=Max(g[i][j],f[i-1][j+b[p]*2]+a[p]);//翻倍 -
            }
        }
        memcpy(f,g,sizeof(g));
    }
    ans=-1e15;
    for (int i=0;i<=k;i++)
        ans=Max(ans,g[k][M]);//k可以不用完
    cout<<ans;
}