概括 & 引言
论文链接🔗:GaussianUDF - CVPR2025
代码链接🔗:https://github.com/lisj575/GaussianUDF
本篇论文也是Shujuan Li今年的CVPR2025,做的是最近很火的3DGS和她擅长的UDF场的内容。
"we propose a novel approach to bridge the gap between 3D Gaussians and UDFs."
"leverage the self-supervision and gradient-based inference to supervise unsigned distances in both near and far area to surfaces."利用自我监督和基于梯度的推理来监督近处和远处到表面的无符号距离。
作者在摘要中提到:
- 现在的3DGS虽然渲染快、表面逼真,但是在3D表示方面它还只是一个有颜色的雾团,而不是一个连续的平滑的几何表面,如果要提取Mesh还是非常困难的;
- 而无符号距离场UDF是一个隐式、连续、以几何为中心的,优点在于很优秀(平滑、连续)表现表面,但训练和渲染慢。
那么这篇论文的挑战就是如何利用离散的、显式的3DGS来学习一个连续的、隐式UDF?
作者提到了两个关键思想:
-
过拟合二维高斯(2D gaussians)
没有用标准的3DGS,而是通过一些手段让3D gaussians变得又薄又平,像一张张二维高斯的薄片。协同优化,利用UDF自身的梯度场来引导“高斯圆盘”对齐到物体表面,而对齐后的高斯又可以来优化UDF -
利用高斯提供监督(Leverage for self-supervision)
一旦物体的表面被这些高斯薄片铺满,那么本身就成了一个非常高质量、关于表面位置的代理(Proxy)。那么这个就是监督信号了,指导UDF的网络的学习,对于空间中任意一点,可以计算它到最近“高斯薄片”的距离,将这个距离作为UDF学习的目标。- 在表面附近:利用对齐好的高斯圆盘的法线方向来监督UDF,贴在表面上那么法线方向就是一个好的近似
- 远离表面的区域:利用UDF自身的梯度场来监督,一般是Eikonal Loss,要求场的梯度大小恒为1
\Vert\nabla u(x) \Vert = 1
还有一个创新的实现方法在于,作者为了让高斯变得又薄又平贴在表面上,作者引入了新颖的约束(novel constraints)来引导3DGS的优化过程。这些约束不仅能够稳定训练,还可以解决UDF学习中一个经常遇到的问题,那就是在物体表面附件(零水平集),梯度场往往很复杂混乱,导致优化困难。通过本文方法可以让梯度场进行有效的规范。
引言方面,首先写出了背景,也就是从NeRF到3DGS的路程,而学习UDF这类隐式场主流方法就是从NeRF进行相结合的,通过体渲染将预测的UDF渲染成图像,再和多视角照片对比作为监督信号,但NeRF效率慢。

Contributions:
- 提出了一种新方法,通过3DGS从多视角图像重建开放表面,以可微分的方式连接了离散高斯和连续UDF。
- 引入了稳定的约束来让高斯“过拟合”到表面上,并设计了新颖的“远近双重”自监督策略来推断无符号距离。
- 在重建具有开放表面和锐利边界的形状方面,取得了当前最先进(state-of-the-art)的成果。
方法
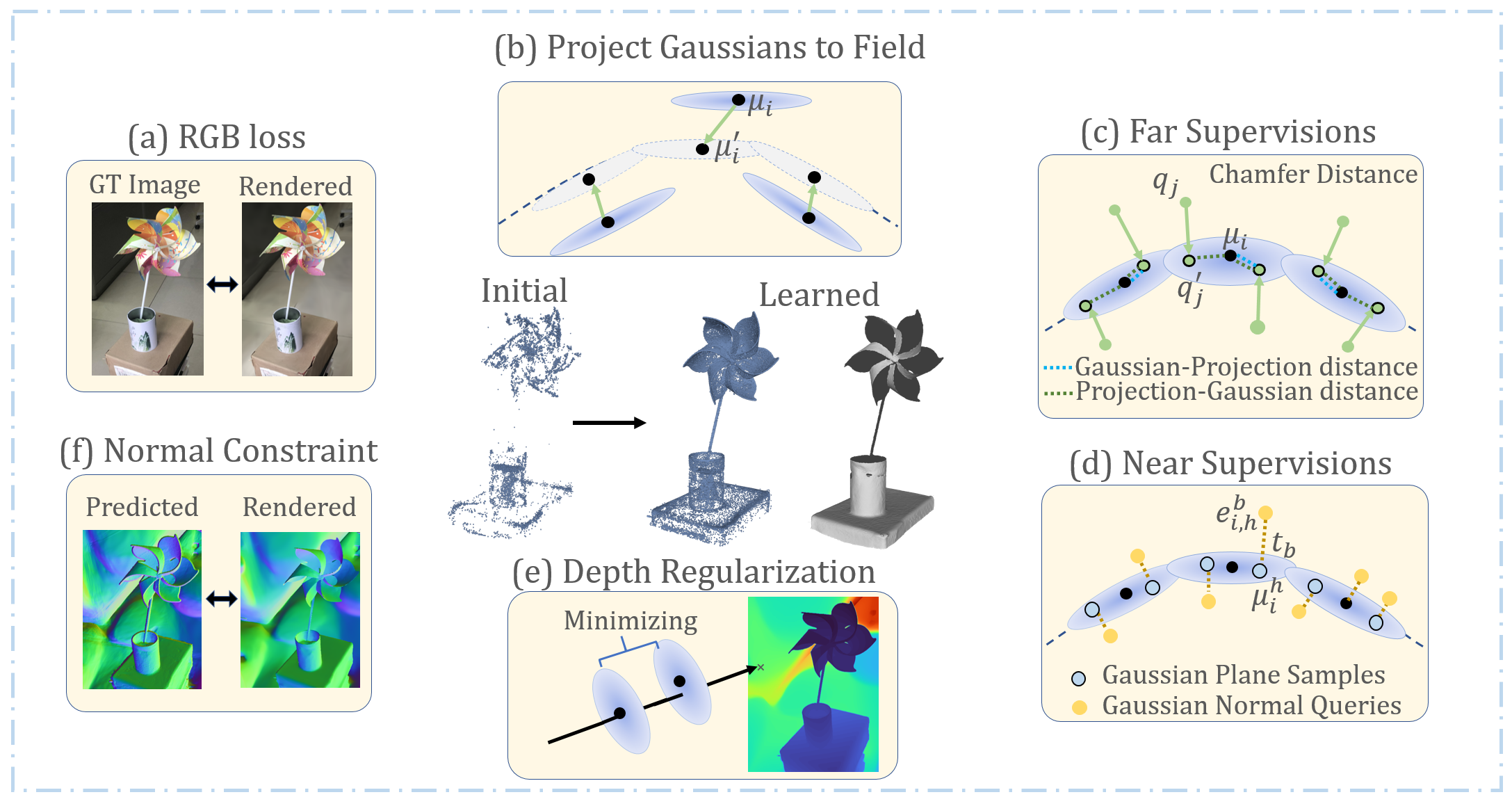
这张图就是这篇论文的灵魂,展示了一个训练和优化的闭环。
- (a) RGB损失。通过调整3D Gaussians的参数,使得渲染图像和真实图像一模一样
- (b) 投影Gaussians到场。在学习之后,2D高斯薄片沿着表面整齐排列。
- (c) 远距离监督。在远离高斯表面的部分,随机采样一些点
q_j,用到最近高斯中心中心点u_i距离来作为粗略真值,监督UDF学习。 - (d) 近距离监督。在高斯附近采样查询点,图中还有法线方向,要求UDF预测的距离值接近于0,这有助于刻画精细、局部的细节。
- (e) 深度正则化。最小化重叠部分。
- (f) 法线约束。要求高斯薄片的法线方向,必须和UDF场在同一位置的法线方向一样。
双向引导(UDF引导高斯、高斯引导UDF),双重监督、正则化约束
💡2D Gaussian Splatting - 基础渲染引擎
高斯参数有如下:位置\mu、定义长宽的缩放因子s、旋转矩阵r(朝向/姿态)、颜色c_i、不透明度\alpha_i
💡法向的来源,这里的法线n_i并不是一个独立的参数,而是从旋转矩阵r决定的。这是合理的,因为一个平面的朝向其实也决定了法线方向n_i
💡渲染方程:
\boldsymbol{C}^{\prime}(u, v)=\sum_{i=1}^{I} \boldsymbol{c}_{i} \alpha_{i} p_{i}(u, v) \prod_{k=1}^{i-1}\left(1-\alpha_{k} p_{k}(u, v)\right),\tag{1}标准的alpha-blending公式,物理意义就是对于屏幕像素(u,v),把会投影到这个像素上的高斯按照深度进行排序,然后像画画一样一层一层根据不透明度混合起来得到最后的颜色。
论文也同样提到一个十分重要的部分,我们把上面参数的颜色c_i换成其他属性,就可以渲染出不同的信息,例如替换成投影距离就可以得到深度图,如图2(e),换成法线就是法线图,如图2(f)。
提到了RGB损失使用的是L_{rgb}=\Vert C'(u,v)-C(u,v)\Vert_1
💡 UDF场
对于一个查询点q我可以得到d=f(q)来获得到表面的距离。而梯度场可以从f推导出来,在q点的梯度\nabla f(q)指向远离最近表面的方向。
而UDF场有一个常见的问题就是,在表面那个距离为的精确分界线上,梯度是未定义的(不可导),就好像|x|的最低点,这属于梯度场混乱的问题。为了解决这个问题,提出了“分而治之”的思想,分为远处监督和近处监督两种:
- 远距离监督(
L_{Far}):
在高斯中心\mu_i附近随机采样J个查询点q_j,进行投影公式q'_j=q_j-d_j\cdot\dfrac{\nabla f(q_j)}{|\nabla f(q_j)|},其中d_j=f(q_j),其实就是表面位置 = 当前位置 - 距离 * 单位法线,这样就到表面上了。损失函数使用的是倒角距离,投影点q'_j到最近高斯中心\mu距离和高斯中心\mu到最近投影点q'_j,直观意义就是投影出来的表面点,作为一个整体,必须和高斯中心\mu要相互靠得近。
\begin{aligned}
L_{f a r}= & \frac{1}{J} \sum_{\boldsymbol{q}^{\prime} \in\left\{\boldsymbol{q}_{j}^{\prime}\right\}} \min _{\boldsymbol{\mu} \in\left\{\boldsymbol{\mu}_{i}\right\}}\left\|\boldsymbol{q}^{\prime}-\boldsymbol{\mu}\right\|_{2}^{2} \\
& +\frac{1}{I} \sum_{\boldsymbol{\mu} \in\left\{\boldsymbol{\mu}_{i}\right\}} \min _{\boldsymbol{q}^{\prime} \in\left\{\boldsymbol{q}_{j}^{\prime}\right\}}\left\|\boldsymbol{\mu}-\boldsymbol{q}^{\prime}\right\|_{2}^{2},
\end{aligned}\tag{4}作者提到这宏观上可以和高斯点骨架保持一致,远离表面的点很有帮助,但有局限性在于仅依赖这个损失是不够的,因为高斯中心点本身可能是稀疏的,无法提供精确的细节。
- 近距离监督(
L_{near})
L_{far}无法描绘精细的细节,但是近距离监督可以。核心思想:利用高斯平面“无中生有”地创造监督数据。已经让2D高斯薄片紧紧贴合在真实表面上,那么此时把这些高斯薄片作为真实表面,创造数据。
公式(5):
L_{near}=\Vert f(e_i^b) - t_b\Vert\tag{5}把创造出来的点e作为输入,喂给UDF网络f,要求输出的f(e)应该必须和此时的标准答案t接近。图中的r_i^h就是第i个高斯薄片上采样的第h个种子点,然后对其进行移动t_b距离,那么得到新点e_{i,h}^b,此时这个点的UDF值就应该是t_b,我对它从法线方向上升t_b,那么它通过UDF也应该下降这么多。
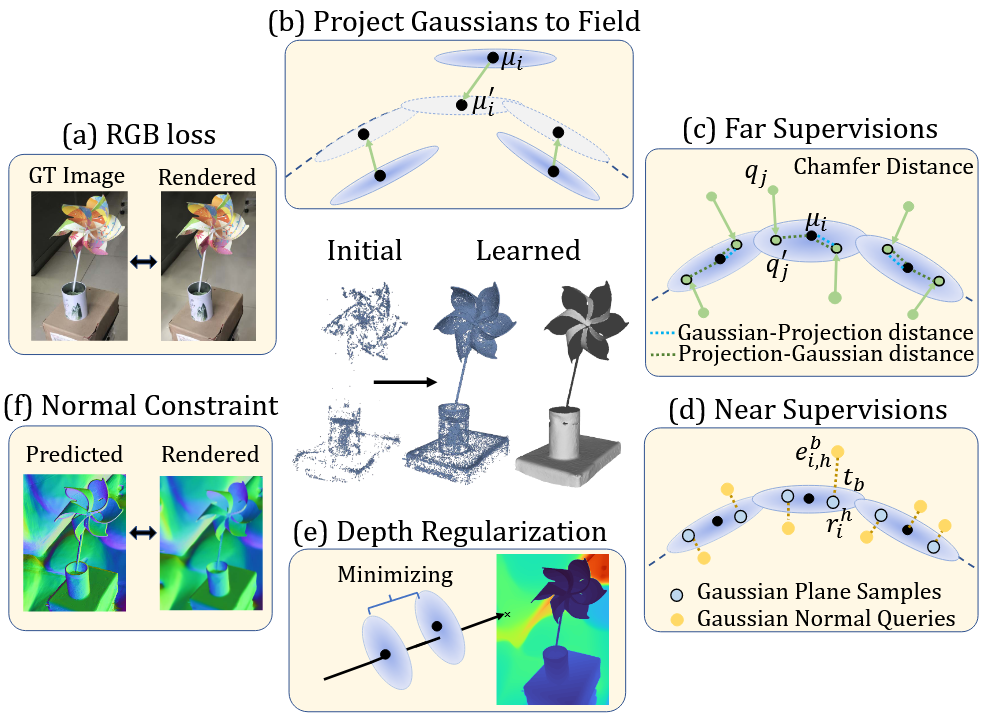
💡过拟合Gaussians到表面
这一部分讲述了图2(b)中将高斯投影到场。我们希望可以将高斯薄片可以紧贴UDF定义的表面上,直观的方法就是,计算出\mu_i的投影点\mu'_i,然后让\mu_i朝着\mu_i'进行移动。但是正如之前所说的,梯度场在表面的时候会十分混乱,不能使用投影公式。作者采用了两步:
- 计算目标,但阻断梯度。通过投影公式来得到
\mu_i',但只取结果而不反向传播。 - 直接拉近。现在
\mu'_i就是一个固定的靶子,直接L2损失拉近。
因为高斯中心并不是在表面上,天真的想法是\mu_{new}=\mu_{old} - f(\mu_{old}) \cdot \dfrac{\nabla f(\mu_{old})}{|\nabla f(\mu_{old})|},但这里梯度并不准确,所以不要一步一步按照梯度来,而是直接利用停止反向传播使用投影公式得到\mu_i'然后通过L2损失拉近
💡 约束深度和法线
这就是图2里面的(e)和(f)中讨论的“深度正则化”和“法线约束”
L_{depth}就是强制高斯形成一个薄薄的单层表面,惩罚同一条相机光路上,前后堆叠的高斯。如果同时看到了两个高斯k1,k2,那么深度值z的差距|z_{k1}-z_{k2}|应该被最小化。
L_{depth}=\sum_{k1,k2}g_{k1}g_{k2}|z_{k1}-z_{k2}|,在这里g_{k1}=\alpha_{k1}p_{k1}(u,v)\prod_{k=1}^{k1-1}(1-\alpha_kp_k(u,b)).
L_{norm}法线一致性损失保证高斯薄片的朝向是正确的,与表面几何一致。根据渲染出来的深度图估算出一个全局的表面法线图,然后要求每一个高斯薄片自身的法线n和位置全局法线N的方向保持一致(通过最大化二者的点击n^TN)
L_{norm} = \sum_kg_k(1-n_k^TN_k).❓N是什么?这里的N是从渲染出来的深度图里估算的法线表面。例如从某个视角渲染出来的深度图D(u,v),这张图的每个像素值代表这个方向上的深度。对于深度图,我们可以计算图像平面上的梯度,即深度u(水平)和v(垂直)方向的变化率:\frac{\part D}{\part u},\frac{\part D}{\part v},然后再反投影回去就可以由2D得到3D的法线向量N了。
❓深度正则化
它并不是把A点和B点在世界坐标系中拉近。而是当从某个视角C看到A和B重叠时,它会惩罚A和B在该视角下的深度差。当从无数个视角都施加这个约束时,就等于迫使所有高斯点形成了一个没有厚度的“薄膜”。这个“薄膜”的形成,并不会因为修正了X方向的视图而破坏Y方向的视图,因为它是满足所有视图约束的最终平衡解。
好,到现在其实差不多了,我们总结一下为什么能够在表面、薄层呢?
- 首先
L_{depth}可以让内部的,堆叠的高斯让其不透明度变低,就像糖葫芦一样只需要第一个,但是这还不足以让其变薄 - 这时候
L_{norm}要求高斯的法线n和宏观法线N一样,就好像方阵教官让每个人的朝向和方阵的朝向一致。这时候就对缩放因子s进行调整,有了明确的n之后调整r去对齐。 L_{near}自监督也会采样点沿着法线移动。L_{rgb}保证了需要保持真实照片,不能随意形状。
💡深度图:
其实就是一张距离地图,看起来像灰度图,但每个像素的数值存储的不是颜色和亮度,而是该像素对应物体表面离相机的距离。通常,像素值越小(颜色越黑)表示距离相机越近,像素值越大(颜色越白)表示距离相机越远。
上面深度差最小的意义在于,不允许在同一个相机视线上存在多个贡献、深度不同的高斯,只保留一个,让后面的透明。当这个规则从所有角度的相机试图上都生效的时候,最终的结果所有不透明的高斯都会自动排列成一个没有厚度的单层曲面。
💡倒角距离:
倒角距离小要求A点云和B点云形态结构相似,比如现在有下面两种情况:
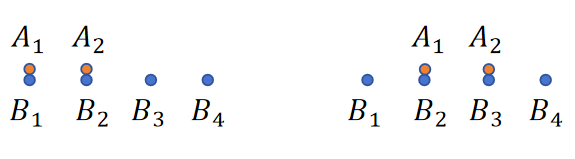
两情况对于A找B来说都是0,但B找A就不一样了,前者是\{0,0,1,2\},但后者是\{1,0,0,1\},前者的倒角距离是\frac{0 + 0}{2}+\frac{0+0+1+2}{4}=0.75,而后者是\frac{0}{0}+\frac{1+0+0+1}{4}=0.5,后者要小,而且直观上后者也更接近。
