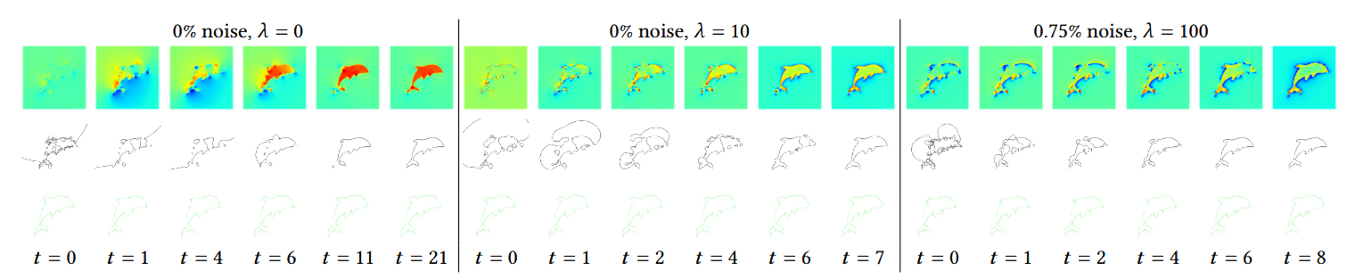
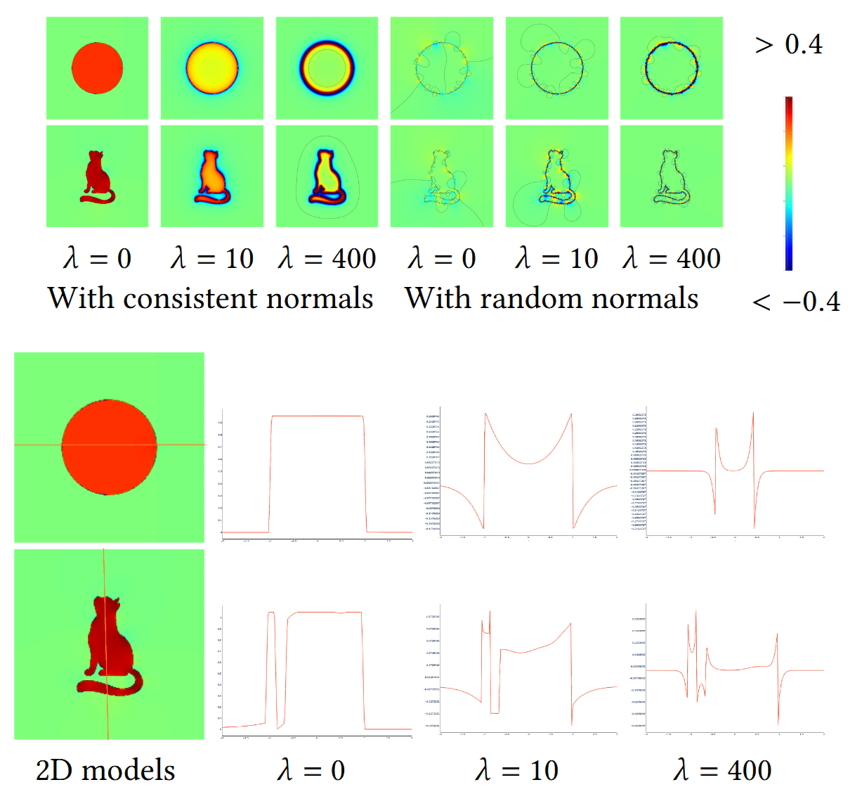
Diffusing Winding Gradients (DWG): A Parallel and Scalable Method for 3D Reconstruction from Unoriented Point Clouds
项目主页🔗:https://dwgtech.github.io/
这篇论文是伟舟师兄发的第二篇CCF-A,发表于TOG2025,也是做法向一致和表面重建的,不对论文进行过多阐述,只详细介绍方法过程。想要看前一篇BIM请见:🔗【法向一致】Consistent Point Orientation for Manifold Surfaces via Boundary Integration
一、前置知识
🔗:卷绕数与广义卷绕数(Winding Number & GWN)
🔗:https://carrynotkarry.com/research/cg/marching-cube/
二、方法
首先回顾广义绕卷数的公式:
w(\mathbf{q})
\;=\;
\frac{1}{4\pi}\,\oint_{S}\mathrm{d}\Omega
\;=\;
\oint_{S}
\frac{\langle \mathbf{x}-\mathbf{q},\,\mathbf{n}_x\rangle}
{4\pi\,\|\mathbf{x}-\mathbf{q}\|^3}\,\mathrm{d}x
公式里面一共有若干个参数,为
- 查询点
q【未知】。也就是我要求解q点的卷绕数是多少 - 点云的点
x【已知】。积分的单元 - 点法线
n_x【已知】。
❓为什么能说点法线n_x已知?我们不是在求解法向一致吗?
这是因为该方法是一个迭代的过程,就像梯度下降法等都会有一个初始的值。特别地,这里我们用n(t)表示第t次迭代的法线n。
下面全文重点来了,整个方法我们一共只有五个步骤:
1️⃣初始化点云
将(N,3)的点云初始化一个随机法线,将(N,6)传入迭代方法中。这就解决了公式里面\mathbf{x}和\mathbf{n_x}
2️⃣计算GWN
通过已知的\mathbf{x}和\mathbf{n_x}得到当前的广义绕卷数GWN,注意这是一个标量场,也就是这个空间内所有的点的GWN都需要求,用体素分成所有的点(类似于切豆腐)。
这样我们得到了一个场的GWN值
3️⃣提取等值面
我们通过GWN值获得一个等值面,注意这里是一个值,即
c=\dfrac{1}{n}\sum_{i=1}^nw(p_i)
即求出流形表面S贡献出来的等值面c。为什么取平均可以认为是等值面呢?
我们可以以二维举例,直观上感受我们应该像求最小二乘法一样得到“等值线”,如图所示:
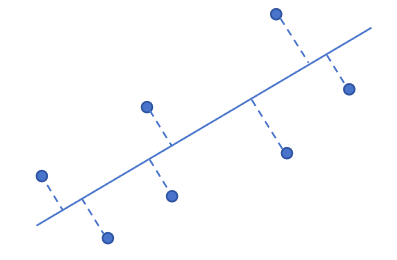
这样肯定做,但是这是一个非线性问题,“等值线”可以是曲线,同样的道理等值面也是如此,那么我们直接取平均来作为等值面
(注意是对流形表面求平均,而不是整个场)
4️⃣更新法向量
既然得到了等值面,我们最终的迭代目标就是如论文公式(4)所示,最终的GWN梯度来近似最终的法向量,即
\mathbf{n_p}(\infty)\approx \nabla w(\mathbf{p},\mathbf{n}(\infty)),\ \forall \mathbf{p}\in\mathcal{S}\tag{4}
那么迭代就是用这一次的GWN梯度代替下一次迭代的法向量,即
\mathbf{n_p}(t+1):= \nabla w(\mathbf{p},\mathbf{n}(t)),\ \forall \mathbf{p}\in\mathcal{S}
那么现在的问题就是:如何求得梯度?
现在已知GWN场(体素),求梯度论文使用的是用三角面片的法线来代替梯度
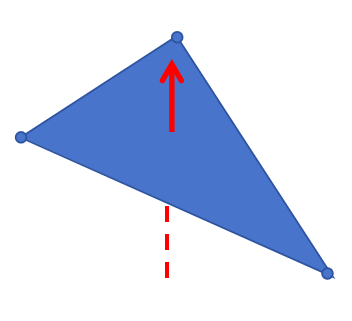
⚠️注意:这里使用的是三角面片的法线,Marching Cube会生成大量的三角面片,但是我们需要的是原始点云上的法线,也就是\mathbf{n_x},那么如何将现在这根红色的法线得到我点云上的法线呢?
投影。没错,就是投影,使用数据结构通过KNN求解得到最近K个点(代码中K=10),然后做投影对其进行贡献,然后对每个点取平均。
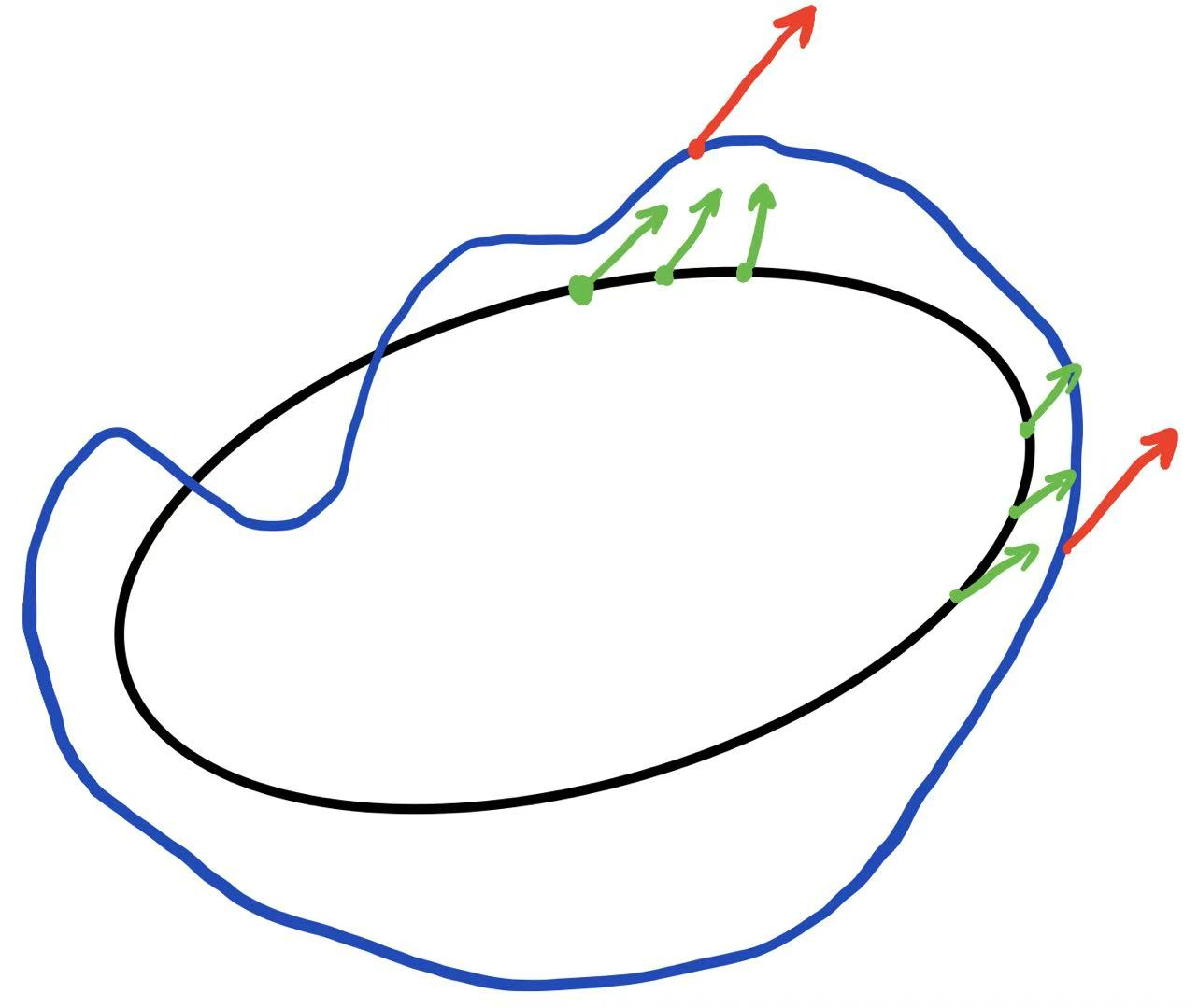
如果图示,黑色⚫的是点云,蓝色🔵是等值面,红色🔴是mesh上的法线(GWN梯度),绿色🟢是最近的K(K=3)个点。
通过这样投影之后,我们取平均便得到了点云上的点法线(用梯度代替的),达到了【更新法向量】的步骤
5️⃣迭代
循环2️⃣3️⃣4️⃣步骤进行迭代,得到n(\infty),最后平均法向不再变化(精度)结束,或者达到最大迭代次数,默认为40次
三、优化
从上面可以看到用了一些数据结构,例如KD-Tree。这里还是用到了八叉树来优化积分。
重新回到公式:
w(\mathbf{q})
\;=\;
\frac{1}{4\pi}\,\oint_{S}\mathrm{d}\Omega
\;=\;
\oint_{S}
\frac{\langle \mathbf{x}-\mathbf{q},\,\mathbf{n}_x\rangle}
{4\pi\,\|\mathbf{x}-\mathbf{q}\|^3}\,\mathrm{d}x
我们假设体素一共分成了m个点,点云一共n个点,对于每一个体素单元都需要使用上面的公式,那么一共需要使用O(m)次,而公式可以看出是对点云上所有的点进行积分,所以每次又需要O(n)次,一共时间复杂度是O(nm)次。
从我的实验中可以看到一个10000个点的点云,最后的点能到400000,那么体素数量m其实远远大于点云上点的个数n。但是这里可以优化一下积分。
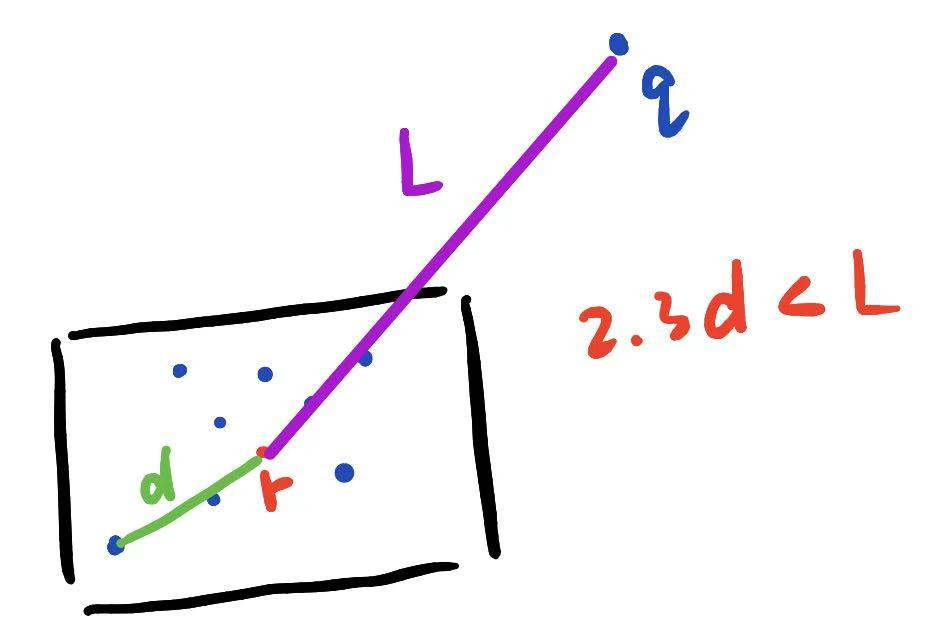
我们使用八叉树(类似于线段树,对空间进行划分),当前八叉树单元中心点r离其中最远点云上点x_i定义为d,如果查询点q举例这个中心点r的距离L大于2.3d,那么就不再往下继续查找,直接使用这个单元中心里面的值。
四、其他
会遇到多个等值面的时候,需要调整λ,论文中有些,λ为超参数