Voronoi图
首先来讲一下维诺图(Voronoi Diagram),主要就是对空间进行剖分,然后对这个几何体进行研究(当然可以二维也可以三维)
看到一个还不错的帖子
【术语(Terminologies)】
- 基点、站点、种子Site:具有一些几何意义的点,比如我做点云的这个就是点云上的点
- 细胞Cell:这个Cell中任意一点到Cell中基点都是最近的,也就是说离其他Site都比离内部Site都要远
- Cell的划分:基点与其他
n-1个点所对应那个平分线(面)所确定的离得更近的那个。把这些所有半平面公共的交集求出来就是这个Cell,所以每个Cell一定是凸的,有些也会是无界的
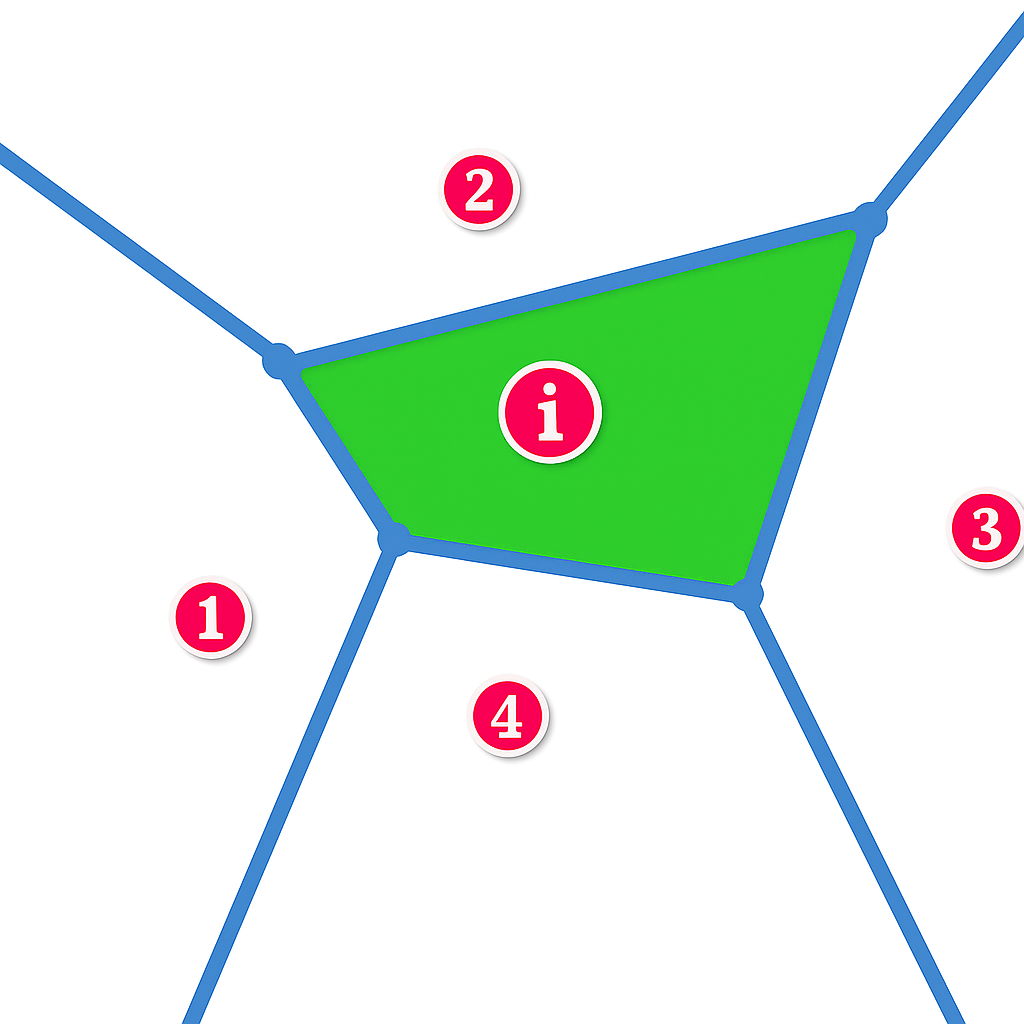
简单而言:
- 首先对于二维平面,我们会对每个点对做垂直平分线。例如1️⃣和4️⃣之间的那条蓝线就是连接1️⃣和4️⃣成为线段,然后对其做垂直平分线
- 最后是所有靠近该点区域的交集,例如1️⃣号点就是很多的垂直平分线最后划分出来的区域,这个区域也一定是凸的
- 那么在三维空间中呢?那就是垂直平分面了,我们常常会在空间中使用这个
Voronoi图中包括Voronoi点(线段与线段之间的交点)、线段Segment、射线Ray或直线,这些线都被称为Voronoi edge
【性质(Properties)】
(1)非空性:每个Site都拥有一个非空的Site
(2)空圆性:在任何一个Site所对应的Cell中,任何一个点以这个点为圆心,以到这个Site的距离为半径的圆必然是空的。
这里的空其实就是这个圆内部不包含任何Site
其实很容易理解,考虑最极端的情况就在边界\Omega^-上,因为靠近于这个垂直平分线,那么到该Cell的Site肯定更接近于旁边那一个,也就是半径为到这个Site的距离的时候,到旁边那个Site还总会差一点的\varepsilon\rightarrow 0
【总结(Conclusion)】
Voronoi划分是一种多边形划分。我们仍然给定平面上一系列点\{P_n\},然后对平面上任意一个点P,找到\{P_n\}中距离当前点P最近的一个点 P_i ,我们就认为P归属于P_i这一类,每一个P_i都有一个自己统辖的区域,这些区域的边界连起来就形成了一个个的凸包,我们就把这些凸包的边当做是对平面的一种分割。

如果从某种视角来看,Voronoi划分的计算过程实际上是完成了机器学习算法中K-Means算法的一次迭代,当然本质上K-Means本来就是一种具有几何意义的分类法。
Delaunay划分
假设我们在平面上有一系列的点的集合 \{P_n\} ,我们对这个点集的凸包(Convex Hull)内部进行三角划分,即每个点都至少属于一个划分得到的三角形,就得到了一系列的三角形的集合 \{T_m\} ,我们求出每个三角形的外接圆,并且要求对于任意一个外接圆,除了位于圆上的三角形的三个顶点外,集合 \{P_n\} 内任何其他点都不能落在这个外接圆内,满足这个条件的三角划分,就是所谓的Delaunay划分。
一张图来直观的看Delaunay划分:

【直观理解】
(1)Delaunay是一种三角剖分(对于二维情况得到的是三角形,对于三维情况得到的是四面体)
(2)这种看起来十分自然且平衡。所谓平衡和自然指的是,这种划分通常不会产生细长的三角形,所有三角形看起来都是相对紧凑的。
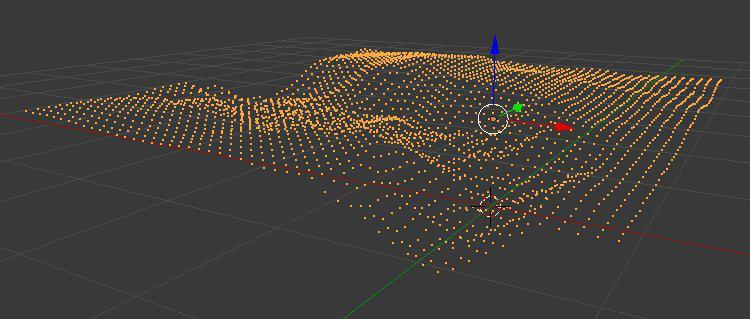
这种划分的作用可以在三维点云中重构出一个地形的三角网格

也有一些风格化的手段,对于2D空间随机生成一些点,然后使用Delaunay划分,对每个划分的三角形内部取重心位置进行色彩填充

Voronoi图和Delaunay划分的联系
对于Voronoi图来说,求出当前点属于哪个凸包是很容易的,至少可以暴力遍历一遍,但是求出Voronoi图的边确是难的。
好消息是:Delaunay图和Voronoi图刚好是对偶图。
如果把Delaunay划分得到的三角形的每个外接圆圆心当作Voronoi图中凸包的顶点,然后对于任意两个外接圆,如果他们贡献Delaunay点集中的两个点(或者说两个Delaunay划分的三角形共享一条边),我们就可以把两个外接圆圆心连起来形成Voronoi图的边,就可以得到相同点集的Voronoi图划分。然后我认为取中点和外接圆圆心做射线即可。
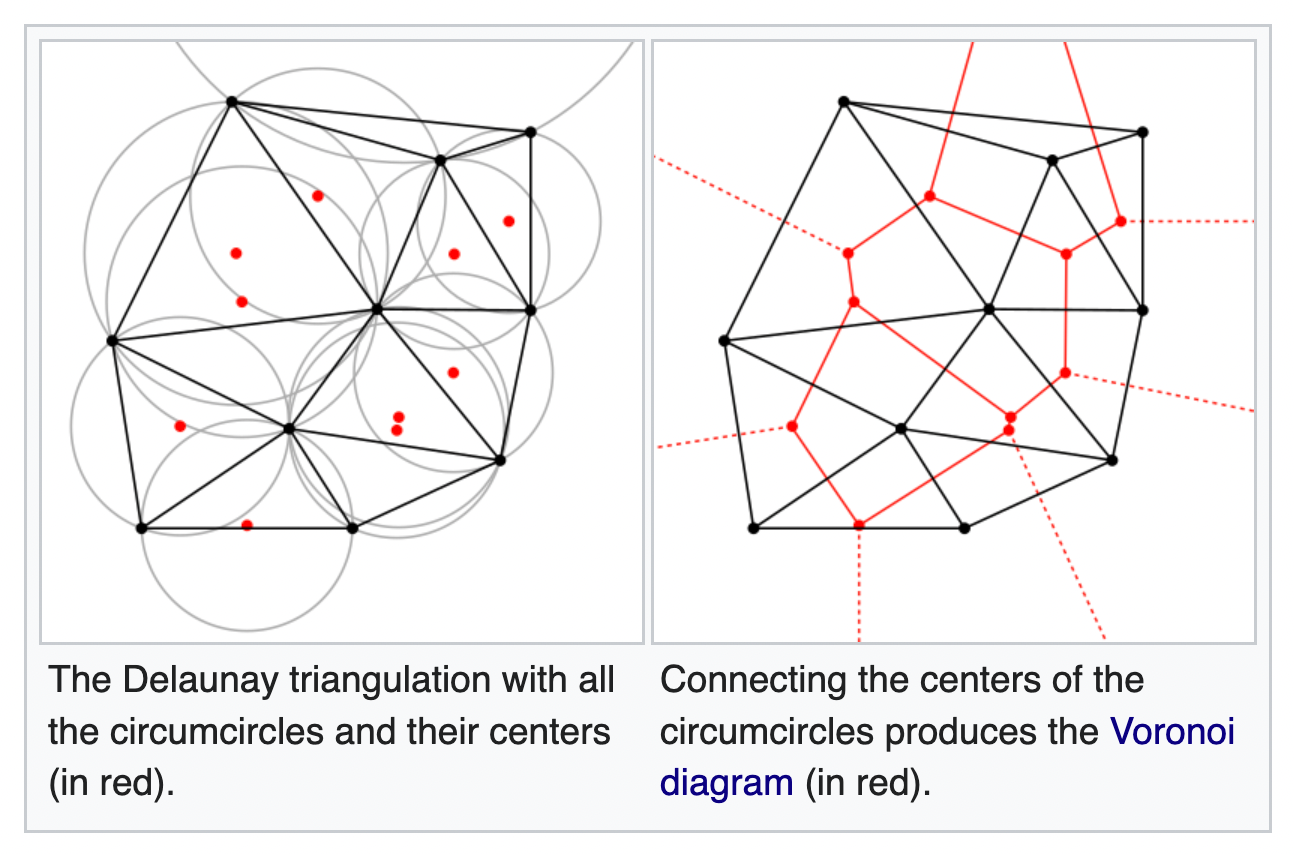
可以看出,Delaunay三角剖分中每个三角形的外接圆圆心其实就是Voronoi图里面的顶点(不是Site,在术语中提到)
利用上述这个思路,我们可以先生成Delaunay图,再根据Delaunay划分得到对应的Voronoi划分。
作用
这里提一下一篇SIGGRAPH的论文,【法向一致】Consistent Point Orientation for Manifold Surfaces via Boundary Integration

Comment