理解三维高斯函数

由于最近在做3DGS相关的内容，要想好好做出来的话还是首先需要搞清楚高斯函数。首先来看看一维二维高斯函数是什么样的

一维高斯函数

一维高斯函数就是我们以前学的正态分布，公式如下：

f(x)
=
\frac{1}{\sqrt{2\pi}\,\sigma}
\exp\!\biggl(-\frac{(x-\mu)^2}{2\sigma^2}\biggr)

我们以\mu = 0, \sigma = 1为例，它的函数图像如下：

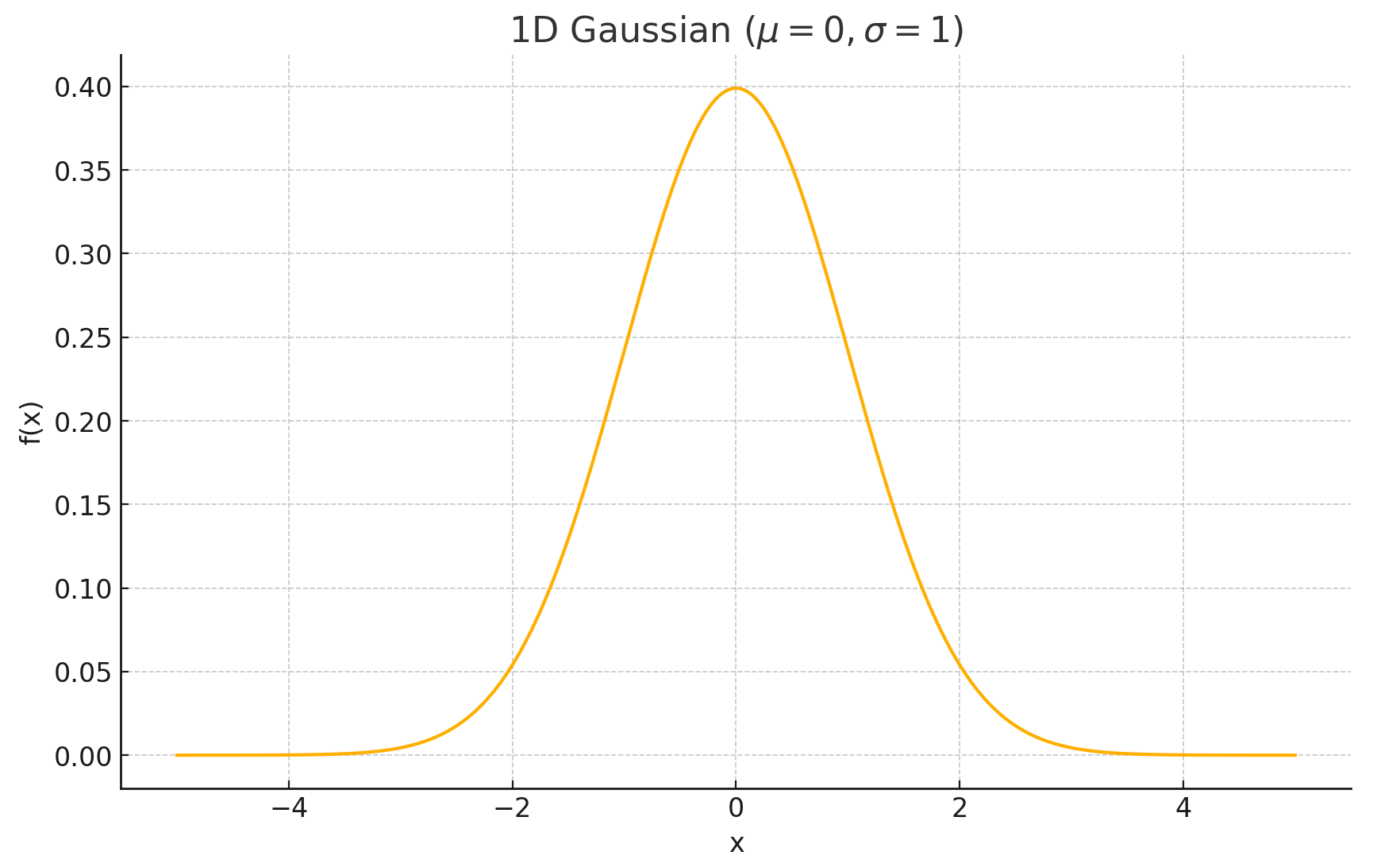
其中\mu是均值，决定曲线的中心，而\sigma是标准差，决定曲线的宽度（即“高矮胖瘦”），我们对其进行积分\int f(x) \ \mathrm{d}x = 1

二维高斯函数

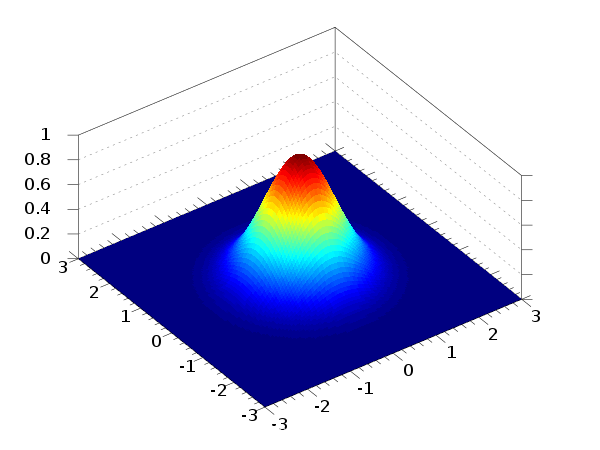
二维高斯函数最简单的轴对齐、可分离形式（\sigma_x,.\sigma_y 各向异），也叫钟型（很像一个钟倒着）

各向异性这里表示的是我对于x,y因为尺度不一样，伸缩的效果也不一样，比如同样放大1.5倍，二者拉伸的长度不一样（换句话说如果是圆就一样了）

f(x,y)
=
\frac{1}{2\pi\,\sigma_x\,\sigma_y}
\exp\!\Biggl(
-\frac{(x-\mu_x)^2}{2\sigma_x^2}
-\frac{(y-\mu_y)^2}{2\sigma_y^2}
\Biggr).

• \mu_x,\mu_y是中心位置坐标
• \sigma_x,\sigma_y分别控制x,y方向上的扩散速度

展示\mu=(0,0),\sigma_x=\sigma_y=1的等高线图（同心椭圆，但这里是圆）

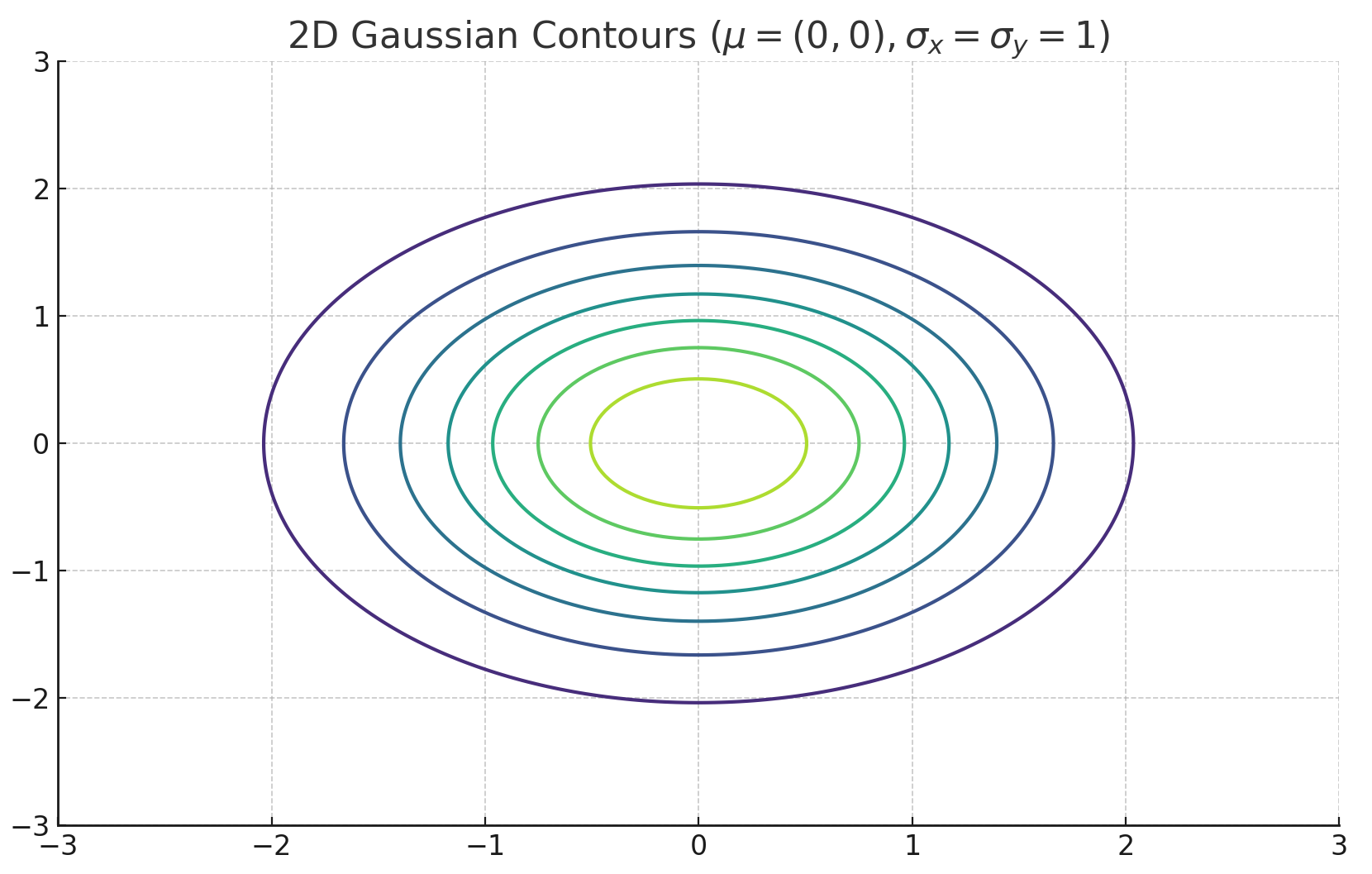
三维高斯函数

首先我们来类比一下

• 在一维中，指数里只有一项(x-\mu)^2/(2\sigma^2)
• 在二维中，指数里增加了第二项(y-\mu_y)^2/(2\sigma_y^2)
• 那么在第三维里，就要增加第三项(z-\mu_z)^2/(2\sigma_z^2)

✨其实可以看到，再来看一下前三张的图。

• 一维高斯函数，我们可以认为是传入一个位置\mathbf{x}=x，可以得到一个概率p=f(x)
• 二维高斯函数，我们可以认为是传入一个位置\mathbf{x}=(x,y)^\mathsf{T}，可以得到一个概率p=f(x,y)，那二维高斯函数的第二张图其实可以用“拟合”去理解，一个底面的x,y往上只能找到一个交点f(x,y)，其实拟合就是一个z=f(x,y)的高度函数。

🔍那么三维是什么样的呢？

我们传入一个位置\mathbf{x}=(x,y,z)^\mathsf{T}，可以得到一个概率p=f(x,y,z)，所以在空间任何一点点一下，我都会得到一个概率p，与二维高斯函数的图2不同的是，虽然那个图也是三维的，但是只会在表面得到一个数值1

f(x,y,z)
=
\frac{1}{(2\pi)^{3/2}\,\sigma_x\,\sigma_y\,\sigma_z}
\exp\!\Bigl(
-(\frac{(\textcolor{red}{x}-\mu_x)^2}{2\sigma_x^2}
+\frac{(\textcolor{red}{y}-\mu_y)^2}{2\sigma_y^2}
+\frac{(\textcolor{red}{z}-\mu_z)^2}{2\sigma_z^2})
\Bigr).

当然，这有一种协方差矩阵的形式，我将推导出来

• 独立分量形式

  假设三维向量 \mathbf{x} = (x, y, z)^\top 各分量独立，分别服从正态分布：

  x \sim \mathcal{N}(\mu_x, \sigma_x^2), \quad
  y \sim \mathcal{N}(\mu_y, \sigma_y^2), \quad
  z \sim \mathcal{N}(\mu_z, \sigma_z^2)

则其联合密度函数为：

  \begin{align*}
  f(x, y, z) &=
  \frac{1}{\sqrt{2\pi}\,\sigma_x}
  \exp\left(-\frac{(x - \mu_x)^2}{2\sigma_x^2}\right)
  \times
  \frac{1}{\sqrt{2\pi}\,\sigma_y}
  \exp\left(-\frac{(y - \mu_y)^2}{2\sigma_y^2}\right) \\
  &\quad \times
  \frac{1}{\sqrt{2\pi}\,\sigma_z}
  \exp\left(-\frac{(z - \mu_z)^2}{2\sigma_z^2}\right) \\
  &=
  \frac{1}{(2\pi)^{3/2}\,\sigma_x\sigma_y\sigma_z}
  \exp\left(
  -\frac{1}{2} \left[
  \frac{(x - \mu_x)^2}{\sigma_x^2}
  + \frac{(y - \mu_y)^2}{\sigma_y^2}
  + \frac{(z - \mu_z)^2}{\sigma_z^2}
  \right]
  \right)\tag{1}
  \end{align*}

• 协方差矩阵形式

  首先写成\mu,\Sigma形式，有：

  \mu =
  \begin{pmatrix}
  \mu_x \\
  \mu_y \\
  \mu_z
  \end{pmatrix},
  \quad
  \Sigma =
  \begin{pmatrix}
  \sigma_x^2 & 0 & 0 \\
  0 & \sigma_y^2 & 0 \\
  0 & 0 & \sigma_z^2
  \end{pmatrix}

指数内部可以写作：

  \frac{(x - \mu_x)^2}{\sigma_x^2}
  + \frac{(y - \mu_y)^2}{\sigma_y^2}
  + \frac{(z - \mu_z)^2}{\sigma_z^2}
  =
  (\mathbf{x} - \mu)^\top \Sigma^{-1} (\mathbf{x} - \mu)

由于 \det \Sigma = \sigma_x^2 \sigma_y^2 \sigma_z^2，密度函数可写成：

  f(\mathbf{x}) =
  \frac{1}{(2\pi)^{3/2}\, \sqrt{\det \Sigma}}
  \exp\left(
  - \frac{1}{2} (\mathbf{x} - \mu)^\top \Sigma^{-1} (\mathbf{x} - \mu)
  \right)\tag{2}

🔍形状为什么是椭球状的呢？是实心对吗？

我们取(2)式的左侧密度值f(\mathbf{x})常数来看，有f(\mathbf{x})=c，然后把\exp左侧的分数乘到左侧，然后经过操作只留下关于\mathbf{x}的部分，有：

\begin{aligned}
c\cdot (2\pi)^{3/2}\, \sqrt{\det \Sigma}&=\exp\left(
- \frac{1}{2} (\mathbf{x} - \mu)^\top \Sigma^{-1} (\mathbf{x} - \mu)
\right)\\
(\mathbf{x} - \mu)^\top \Sigma^{-1} (\mathbf{x} - \mu) &= -2\ln \left( c\cdot (2\pi)^{3/2}\, \sqrt{\det \Sigma}
\right)\\
&= d\gt 0
\end{aligned}

这正是中心为\mathbf{\mu}满足二次型

(\mathbf{x} - \mu)^\top \Sigma^{-1} (\mathbf{x} - \mu)=d

的椭圆面。

对于\exp前面的东西为什么是这样的，其实分母是归一化因子，这样进行积分可以得到1.

协方差矩阵

写在前面：协方差矩阵其实一直都挺难理解的，因为我一直学的不精，这里稍微多思考思考，毕竟还是很重要的

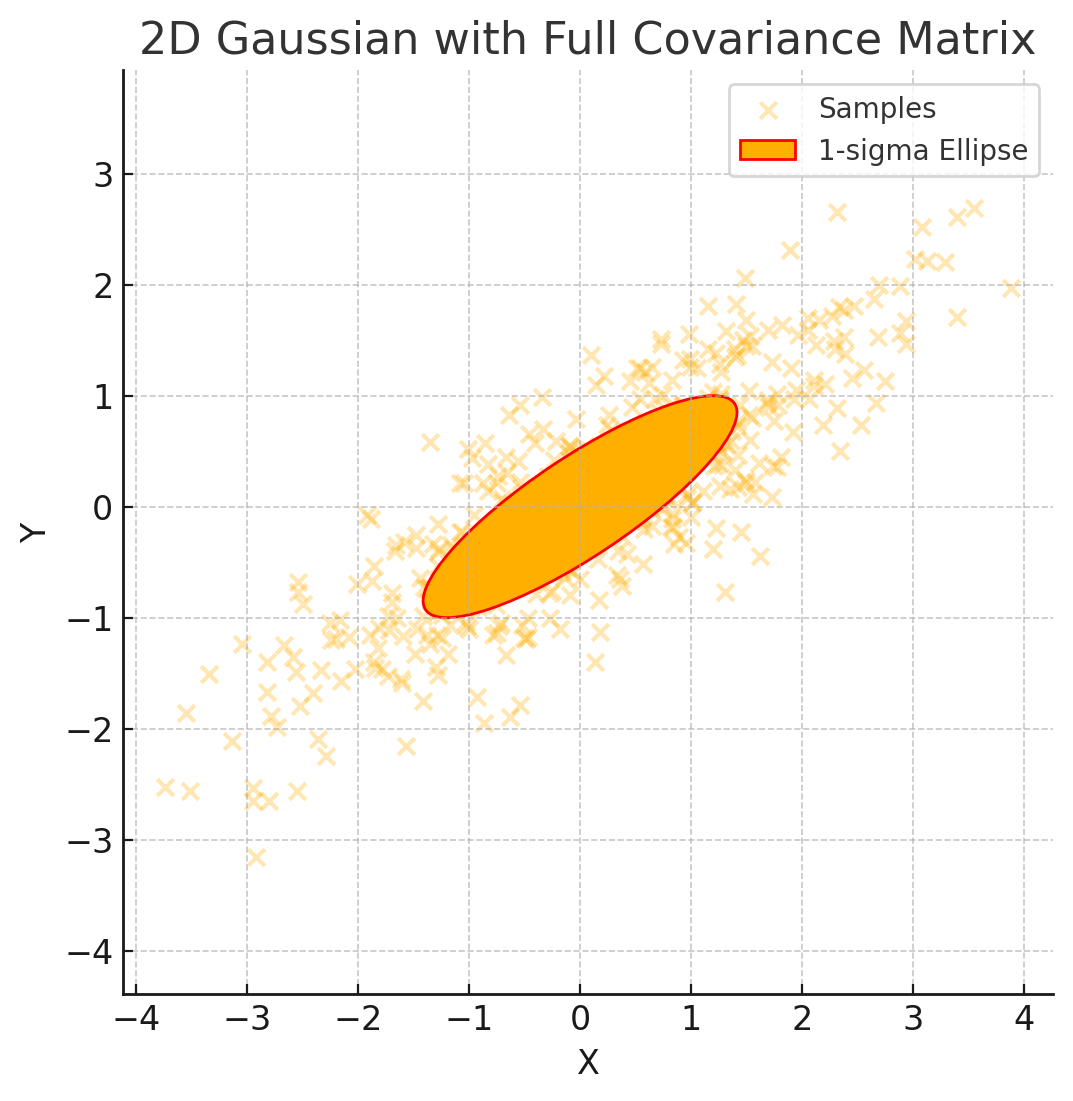
这里以二维高斯函数为例，请思考一下这里的协方差矩阵是什么样的？当然是一个2\times 2的矩阵，每一项是什么样的，表示什么意义？

答案在这，对于二维随机变量(X,Y)，协方差矩阵写作：

\Sigma = \begin{bmatrix}  \sigma_X^2 & \mathrm{Cov}(X,Y)\\
\mathrm{Cov}(Y,X) & \sigma_Y^2

\end{bmatrix}

其中：

• \sigma_X^2：变量X的方差 → 控制水平方向（X轴）上的扩散；
• σ_Y^2：变量 Y 的方差 → 控制垂直方向（Y轴）上的扩散；
• \mathrm{Cov}(X,Y)：变量X与Y的协方差 → 控制旋转倾斜角度（两个变量是否一起增大或减小）

请再次注意上面加粗的字，【方差】、【旋转倾斜】

那么\mathrm{Cov}(X,Y)对应的三种情况如下图：

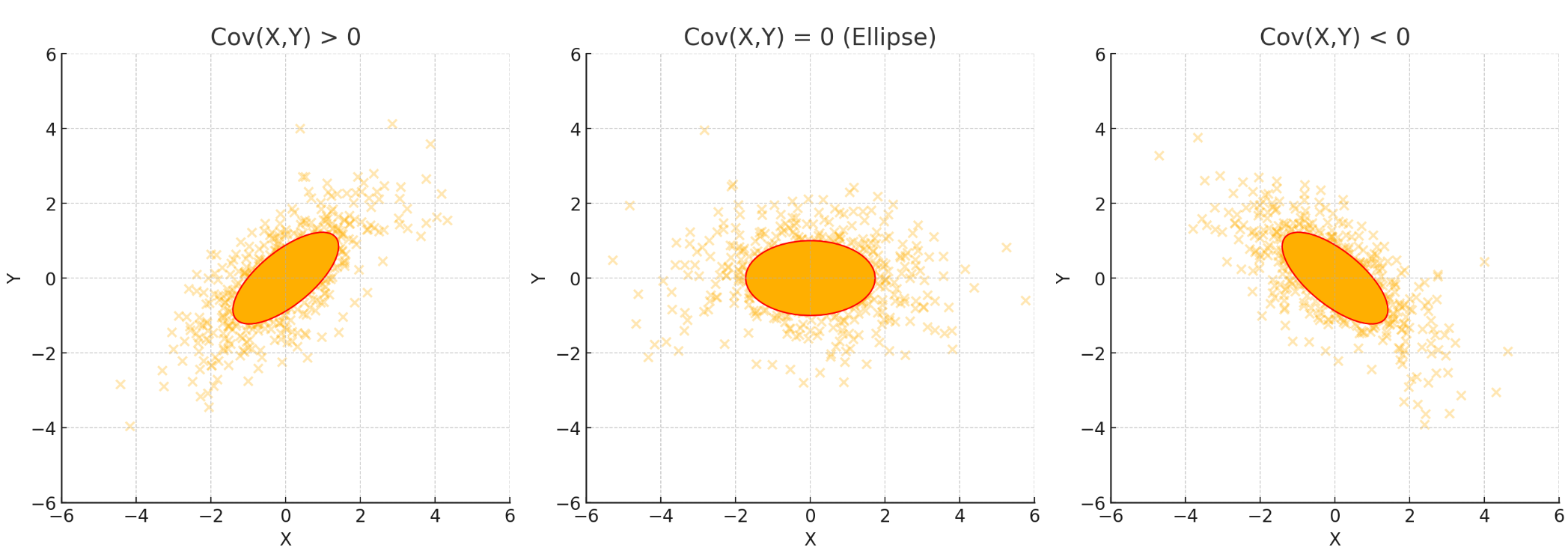
值得一提的是，中间表示的是\mathrm{Cov}(X,Y)=0的情况下，这里\mathrm{Var}(X)=3.0,\mathrm{Var}(Y)=1.0，没有相关性但是每个维度扩散程度不一样所以呈现的椭圆，这里也体现了各向异性。其他两种情况表示的正相关和负相关

\mathrm{Var}(X)=\mathbb{E}[(X-\mu_x)^2]，即方差(Variance)，衡量一个变量的“波动程度”，方差越大越扁

多维高斯函数性质

因为三维高斯函数画不出来，首先我描述一下我所理解的，因为我们把密度看成一个常数，所以它就像一个洋葱一样，外面一层是概率密度最小的，然后内部是最大的一层，所以是一个实心球。这让我想到一首歌：

如果你愿意一层一层

一层地剥开我的心

——《洋葱》杨宗纬

接着我们来看一下协方差矩阵对应不同的值的情况（以二维高斯函数为例）

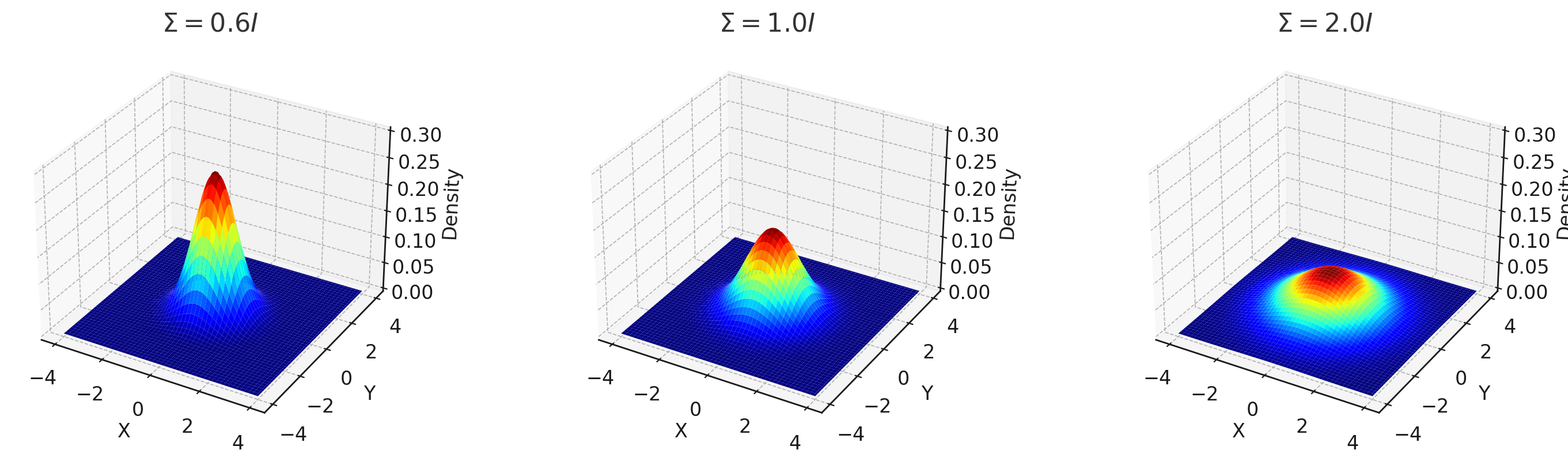
上面三个图像的位置（期望）都是\mu =[0,0]^\top

• 左图：\Sigma = 0.6I。瘦高，方差小，波动范围小
• 中图：\Sigma = 1.0I。均衡
• 右图：\Sigma = 2.0I。扁平，方差大，波动范围大

从数学方面可以理解为对于(2)式中

• \Sigma越大，\Sigma^{-1}越小 → 指数衰减越慢，分布变宽；
• 同时归一项\sqrt{\det \Sigma}^{-1}变小 → 峰值密度下降

如果协方差矩阵不是对角矩阵呢（逆对角上有值）？

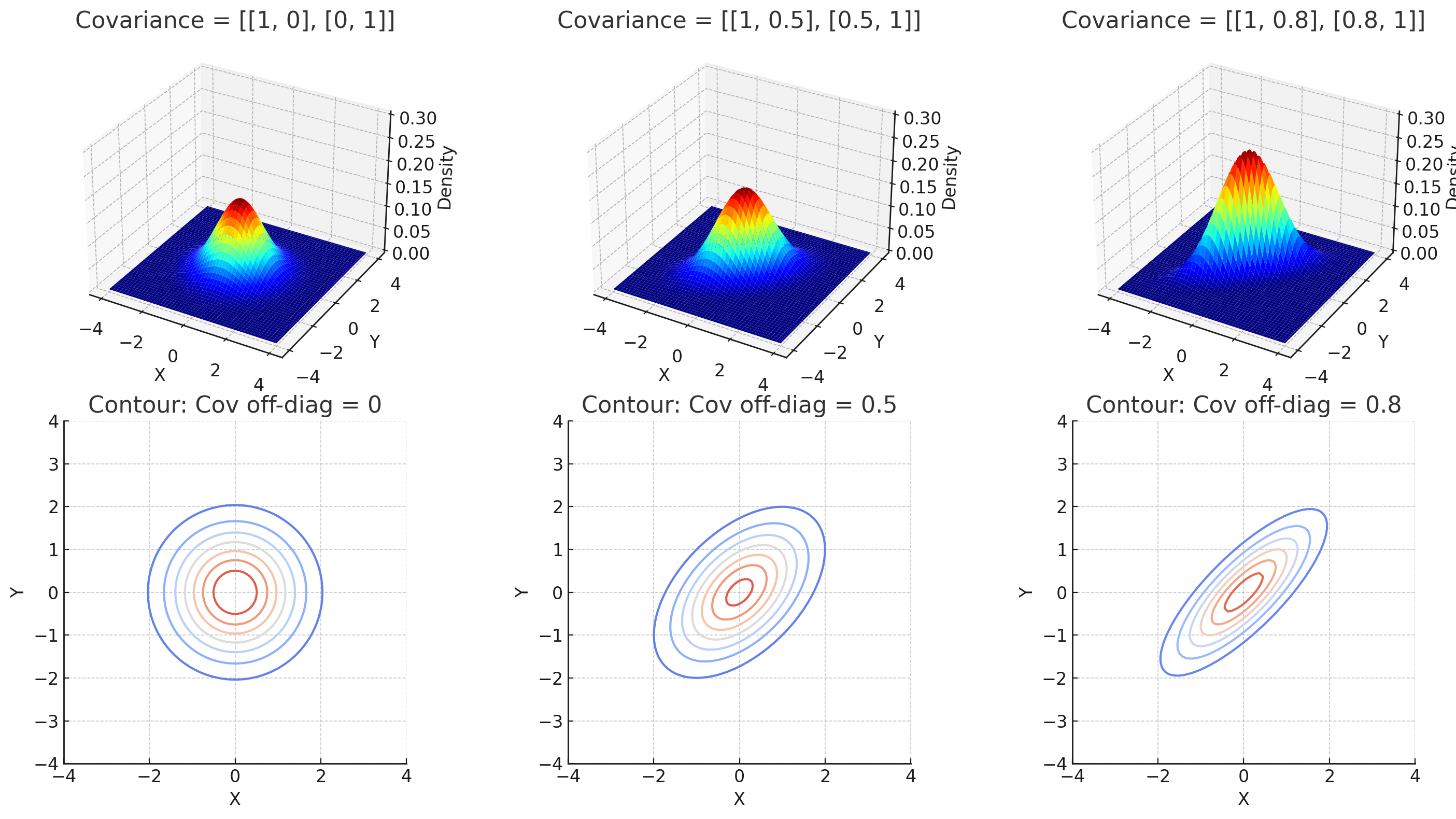
现在协方差矩阵是：

\Sigma = \begin{bmatrix}
1 & \rho \\
\rho & 1\\
\end{bmatrix}, \text{  其中}\rho\in\{0, 0,5, 0.8\}

• 右图\rho=0.8：强相关；

  椭圆非常“扁平”，主轴明显对角线倾斜；

  说明大多数样本点在 x=y 附近，表示两个变量的共同涨落趋势极强。

协方差大于的时候，椭圆倾斜，因为此时正相关