深度学习之前向传播和反向传播

写在前面

以前对深度学习这些（特别是正向传播和反向传播）一知半解的，今天在看3DGS的Cuda代码的时候看到了一些梯度求导，我很纳闷这些不是可以给优化器去算的吗？以及我要用什么对什么求导，以及那些链式法则等，现在大概都搞懂了，这里也会持续更新。

这里用回归一个\hat{y}=wx+b进行举例，首先获得样本数据

# 生成样本数据
x = torch.linspace(0, 1, 100).unsqueeze(1)  # (100, 1)
true_w, true_b = 2.0, 1.0
y = true_w * x + true_b + 0.1 * torch.randn_like(x)

使用的损失函数是均方误差:

\mathcal{L}=\dfrac{1}{N}\sum_{i=1}^N(\hat{y}_i-y_i)^2

所以我们定义模型：

# 定义模型
model = nn.Linear(1, 1)
loss_fn = nn.MSELoss()
lr = 0.1 # 学习率，即步长，每一步走多远

代码放在了：https://paste.org.cn/bi7QdwbM3A

正向传播

我理解的正向传播主要就是去预测结果，并且计算loss，如下面的代码：

for epoch in range(50):
    y_pred = model(x)                  # 正向传播
    loss = loss_fn(y_pred, y)          # 计算 loss

这是很经典的首先推测出y_pred，然后计算loss，可以说仅此而已。我们同时把迭代的代码写出来，可以很清楚的看到：

for epoch in range(50):
    # = 正向传播 =
    y_pred = model(x)
    loss = loss_fn(y_pred, y)

    # = 反向传播 =
    if manual_grad:
        model.zero_grad()

        # 手动计算 dL/dy_pred
        grad_output = 2 * (y_pred - y) / y.size(0)

        # dL/dW = dL/dy_pred * dy_pred/dW
        grad_w = (grad_output * x).sum()
        grad_b = grad_output.sum()

        with torch.no_grad():
            model.weight -= lr * grad_w
            model.bias -= lr * grad_b
    else:
        model.zero_grad()
        loss.backward()
        with torch.no_grad():
            for param in model.parameters():
                param -= lr * param.grad

反向传播

反向传播指的是计算神经网络参数梯度的方法。反向传播里面依赖链式法则，因为中间可能有很多层，比如Y=f(X)和Z=g(Y)，那么链式法则就是：

\dfrac{\part Z}{\part X}=\text{prod}\left( \dfrac{\part Z}{\part Y} , \dfrac{\part Y}{\part X}\right)

➤ 1️⃣ 自动求导

首先我要指出的是，正如上方的代码所示我们可以通过loss.backward()去自动计算模型里面的参数w,b的导数，然后对于model里面的参数进行更新：

    model.zero_grad() # 清空梯度
    loss.backward()
    with torch.no_grad():
        for param in model.parameters():
            param -= lr * param.grad

➤ 2️⃣ 手动求导

我们可以再看一下均方误差以及参数和\hat{y}之间的联系

\begin{aligned}
\hat{y}&=wx+b\\
\mathcal{L}&=\dfrac{1}{N}\sum_{i=1}^N(\hat{y}_i-y_i)^2
\end{aligned}

既然我们要准确，那么要把选择的损失函数最小化，那么什么影响损失函数的变化呢？

那么对于\mathcal{L}而言肯定是\hat{y}在影响，那么什么影响\hat{y}呢，就是我们的参数w,b，这里的值都存放在了model = nn.Linear(1,1)中，可以用model.weight和model.bias进行调用更新。

为了方便，我这里首先写出\mathcal{L}对\hat{y}的梯度，方便

\begin{aligned}
\dfrac{\part\mathcal{L}}{\part \hat{y}}&=\dfrac{\part \left(\dfrac{1}{N}\sum_{i=1}^N(\hat{y}_i-y_i)^2\right) }{\part \hat{y}}\\
&=\dfrac{1}{N}\sum_{i=1}^N2(\hat{y}_i-y_i)
\end{aligned}

所以我们要求出w,b对\mathcal{L}的影响就要用到链式法则：

\begin{aligned}
\dfrac{\part\mathcal{L}}{\part w}&=\dfrac{\part\mathcal{L}}{\part \hat{y}}\cdot\dfrac{\part\mathcal{\hat{y}}}{\part w}\\
&=\dfrac{1}{N}\sum_{i=1}^N2(\hat{y}_i-y_i)\cdot x
\\
\dfrac{\part\mathcal{L}}{\part b}&=\dfrac{\part\mathcal{L}}{\part \hat{y}}\cdot\dfrac{\part\mathcal{\hat{y}}}{\part b}\\
&=\dfrac{1}{N}\sum_{i=1}^N2(\hat{y}_i-y_i)\cdot 1

\end{aligned}

所以在迭代中，代码就可以写成这样：

for epoch in range(50):
    # = 正向传播 =
    y_pred = model(x)
    loss = loss_fn(y_pred, y)
    loss_list.append(loss.item())

    # = 反向传播 =
    if manual_grad:
        model.zero_grad()

        # 手动计算 dL/dy_pred
        grad_output = 2 * (y_pred - y) / y.size(0)

        # dL/dW = dL/dy_pred * dy_pred/dW
        grad_w = (grad_output * x).sum()
        grad_b = grad_output.sum()

        # 更新
        with torch.no_grad():
            model.weight -= lr * grad_w
            model.bias -= lr * grad_b

可视化

我们可视化一下上面的代码，经过50次迭代的结果如下：

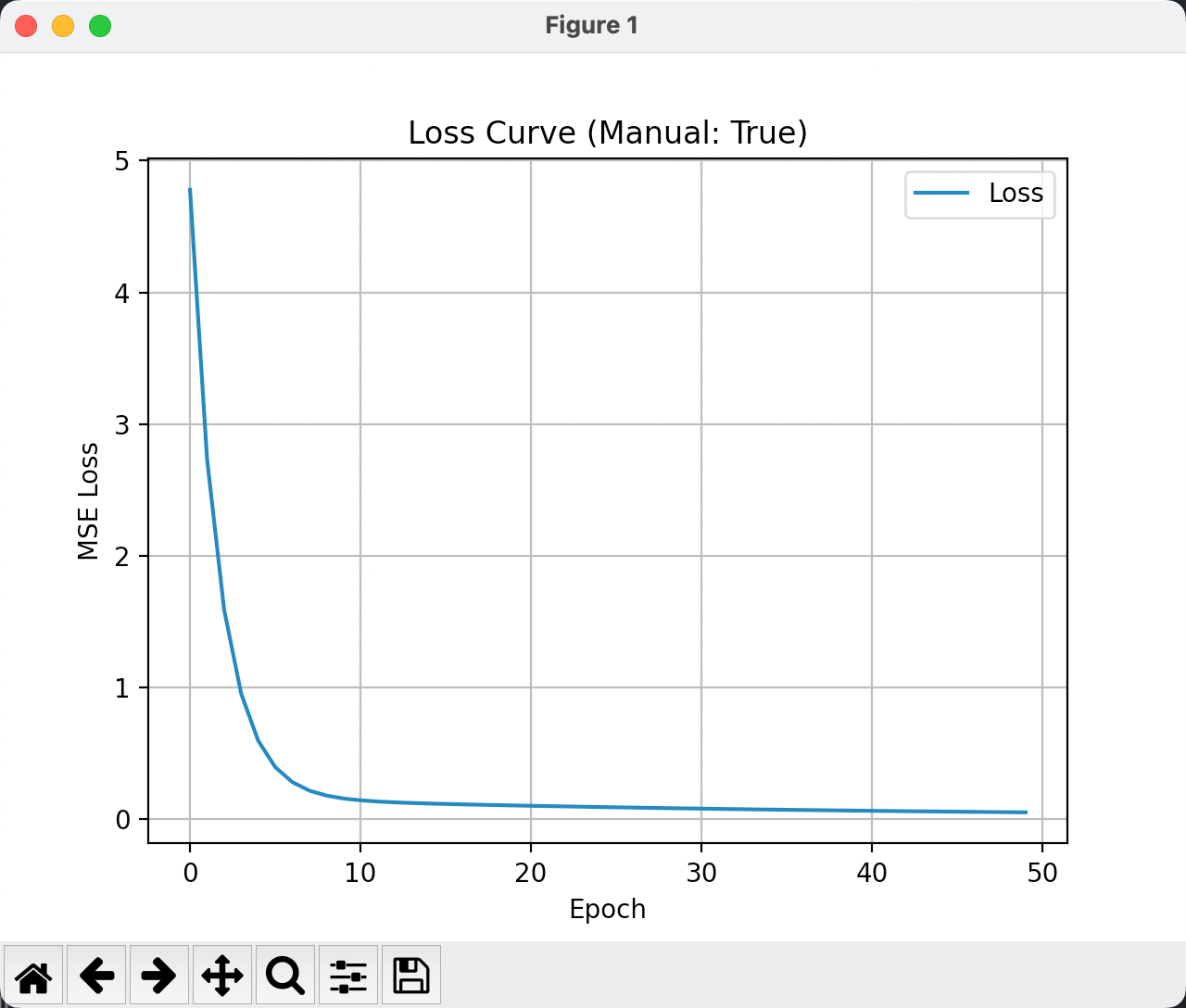
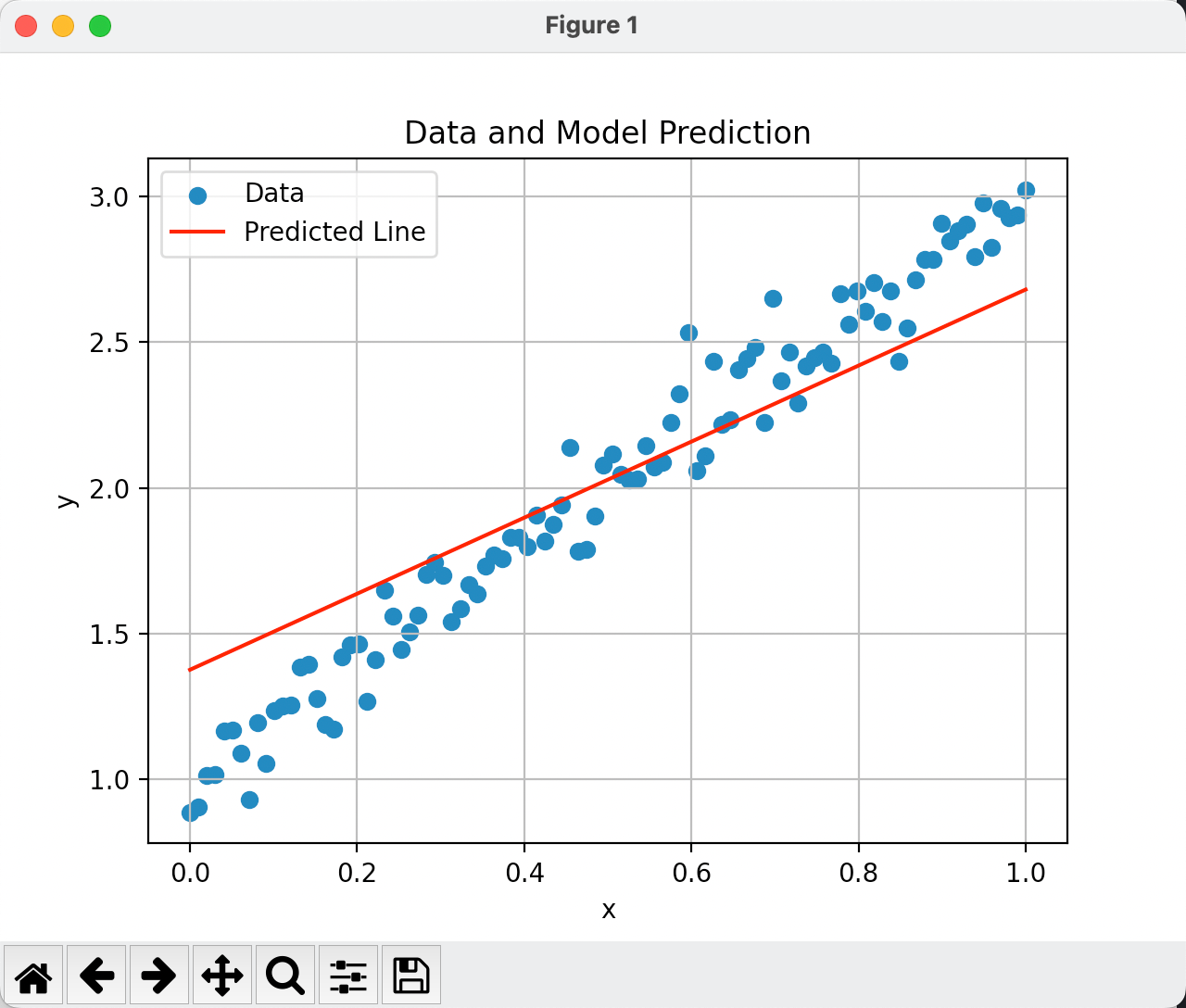
输出结果可以看到：

True w:  2.0
True b:  1.0
Learned w:  1.3135614395141602
Learned b:  1.3715894222259521

Adam优化器

Adam（Adaptive Moment Estimation） 是一种非常流行的深度学习优化器，它结合了：

• Momentum（动量）：历史梯度方向的“惯性”
• RMSProp（自适应学习率）：对每个参数单独调整学习率

⚙️ 直觉理解:

Adam 会对每个参数：

1. 记录“过去的平均梯度”方向（动量）
2. 跟踪“梯度的平方”用于自适应缩放
3. 然后智能地调整步子大小和方向 ✅

而Adam优化器的代码如下：

# 开始训练
for epoch in range(50):
    y_pred = model(x)             # 正向传播
    loss = loss_fn(y_pred, y)     # 计算 MSE Loss
    loss_list.append(loss.item())

    optimizer.zero_grad()         # 清空旧梯度
    loss.backward()               # 反向传播，自动求导
    optimizer.step()              # 用 Adam 更新参数

我们可视化一下结果，训练50次的epoch结果如下：

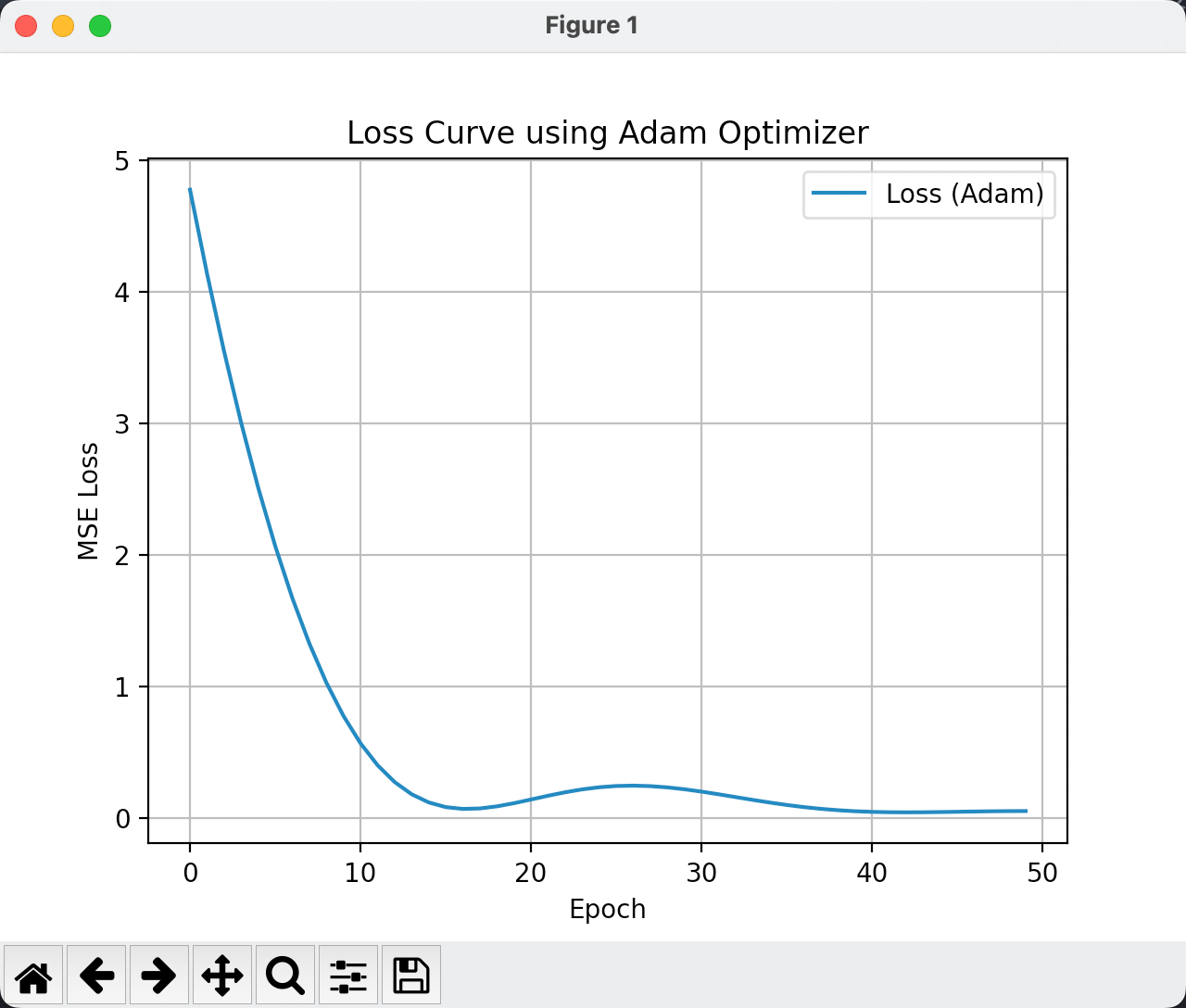
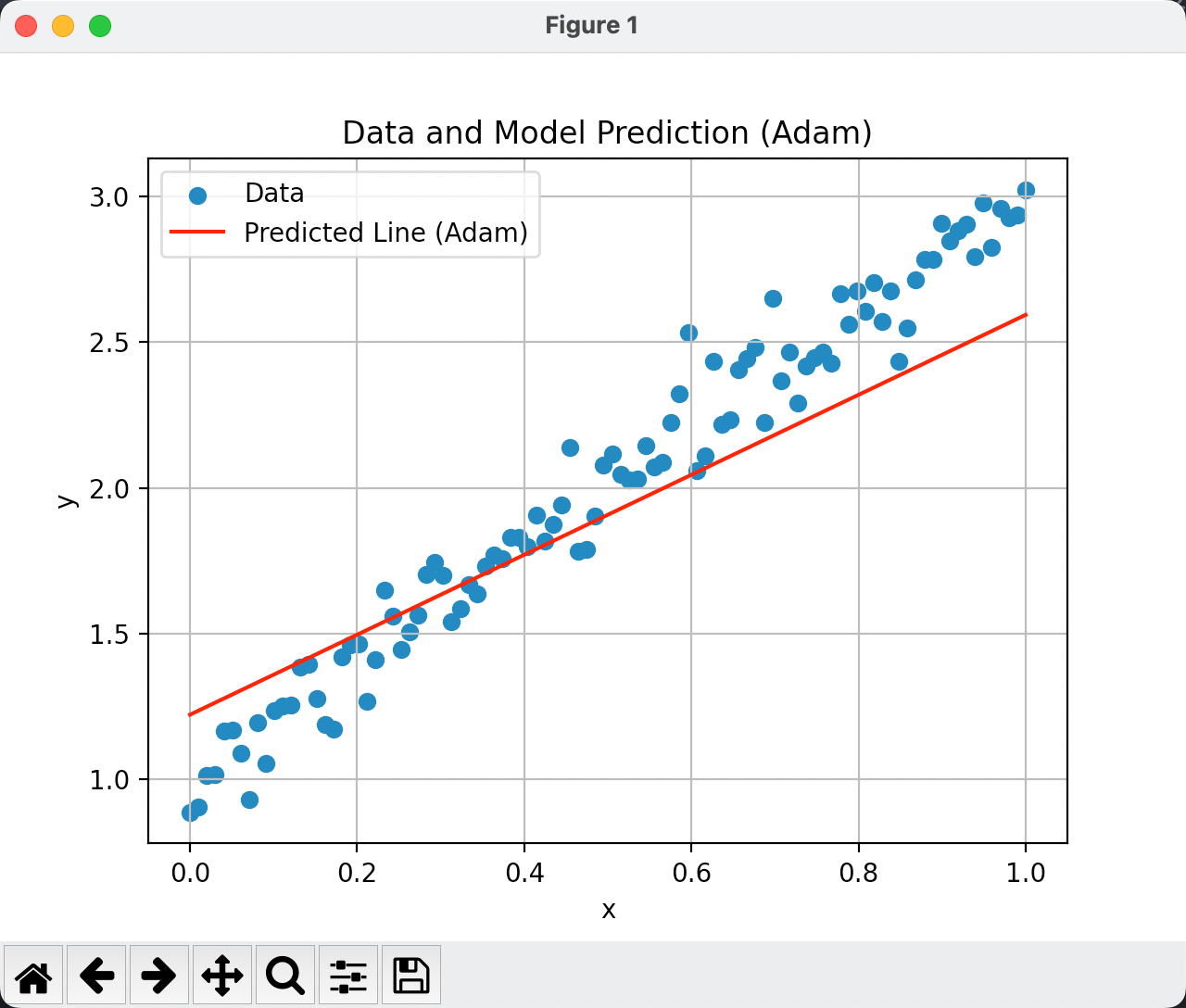
输出为：

True w:  2.0
True b:  1.0
Learned w:  1.378663420677185
Learned b:  1.2160416841506958

思考

问题1️⃣： 为什么学习到的w和b不是接近于1和2呢？明显直线没有穿过样本。

我们通过学习的epoch轮次和学习率lr来考虑，这里是轮次较低导致的，我们训练300次的结果可以看出：

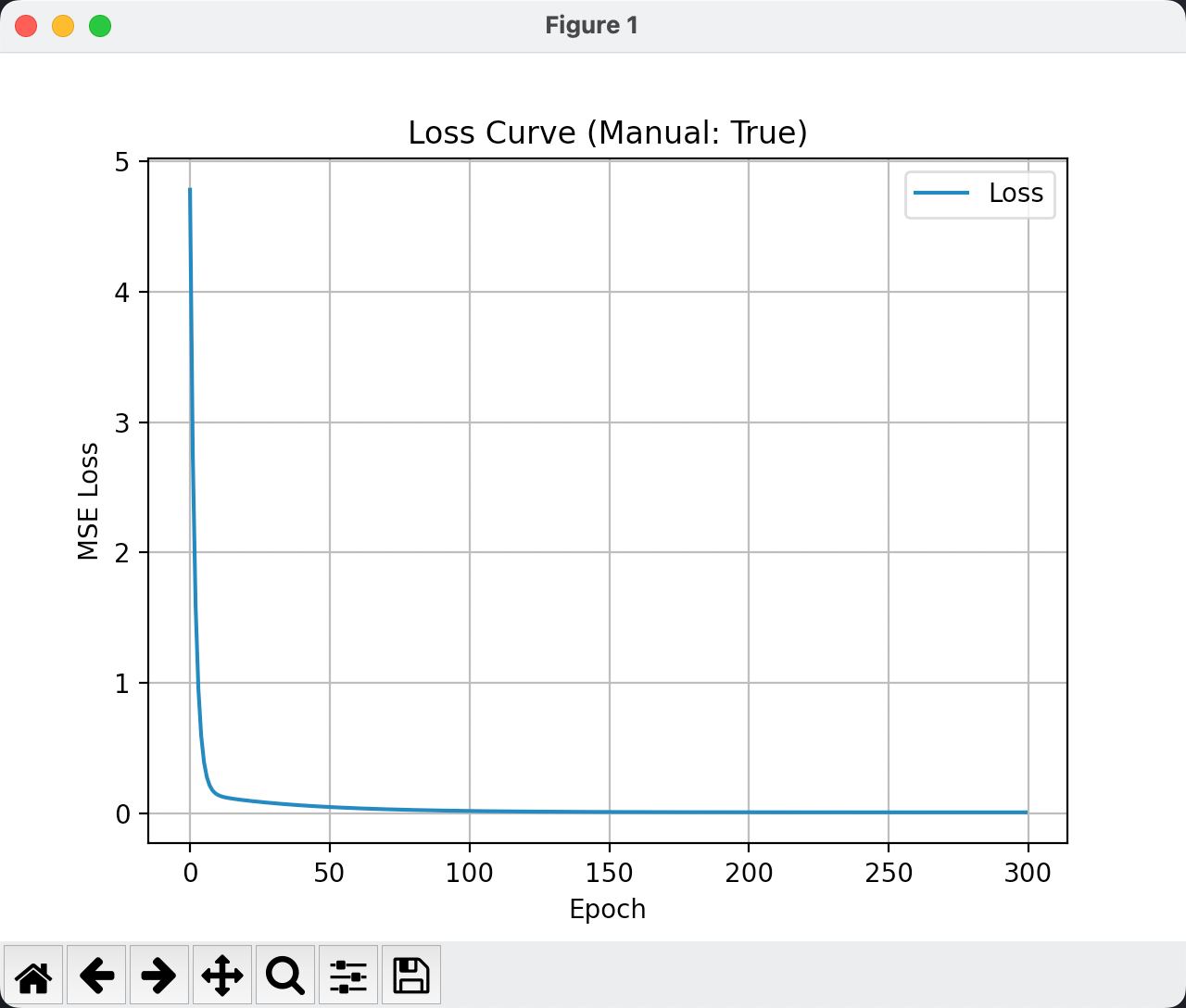
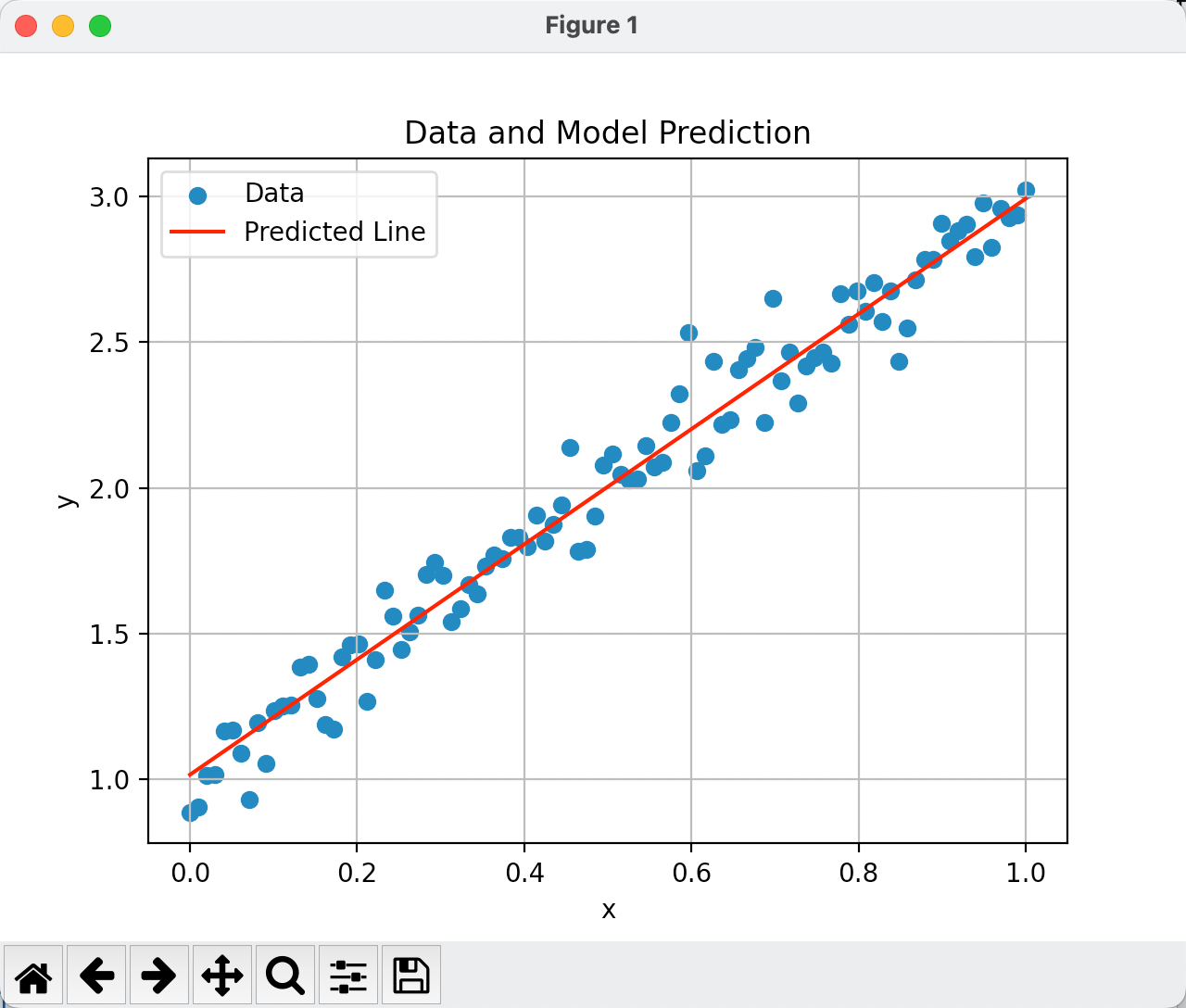
问题2️⃣：nn.Linear(in, out) 对应的数学公式是什么？

🔸 1. nn.Linear(1, 1)

数学公式：

y = w_1 x + b

🔸 2. nn.Linear(1, 2)

数学公式：

\begin{aligned}
y_1 &= w_{11} x + b_1 \\
y_2 &= w_{21} x + b_2
\end{aligned}

🔸 3. nn.Linear(2, 1)

数学公式：

y = w_1 x_1 + w_2 x_2 + b

🔸 4. nn.Linear(2, 2)

数学公式：

\begin{aligned}
y_1 &= w_{11}x_1 + w_{12}x_2 + b_1 \\
y_2 &= w_{21}x_1 + w_{22}x_2 + b_2
\end{aligned}

🔸 5. nn.Linear(2, 3)

数学公式：

\begin{aligned}
y_1 &= w_{11}x_1 + w_{12}x_2 + b_1 \\
y_2 &= w_{21}x_1 + w_{22}x_2 + b_2 \\
y_3 &= w_{31}x_1 + w_{32}x_2 + b_3
\end{aligned}

对于 nn.Linear(in_features, out_features)：

• 权重是 \text{out\_features} \times \text{in\_features} 的矩阵
• 偏置是 \text{out\_features} 的向量