【统计流形】A Statistical Manifold Framework for Point Cloud Data

2025年3月13日 下午4:05 科研 , ,

A Statistical Manifold Framework for Point Cloud Data

1. Introduction

自编码器的两种应用

简介

  • 3D形状变形

应用 1：3D 形状变形（Shape Morphing）

  • 目标：平滑地将一个 3D 形状（如圆柱）变形为另一个 3D 形状（如圆锥）。
  • 方法：
    • 训练一个 自编码器（Autoencoder），将 3D 点云（圆柱和圆锥）映射到一个低维的潜在空间（Latent Space）。
    • 在这个潜在空间中，使用 黎曼度量（Riemannian Metric） 计算最小测地线（Minimal Geodesic）。
    • 通过测地线插值来平滑变形圆柱到圆锥，而不是简单的线性插值。
  • 结论：这种基于黎曼度量的形状演化比在潜在空间中直接进行线性插值更加自然和直观。

举例：

  • 传统的线性插值可能会导致中间形态看起来不自然，例如圆柱逐渐塌缩成一个扭曲的形状，而不是平滑地变成圆锥。

  • 统计流形上的测地线插值可以更好地保持形状特征，使得中间形态在几何上更加合理。

  • [x] 应用 2：学习最优潜在空间坐标（Optimal Latent Space Representation）

  • 目标：找到一个最佳的潜在空间坐标系，使得：

    • 欧几里得直线可以很好地逼近统计流形上的最短测地线。
    • 这个潜在表示可以更好地保留数据的几何结构，从而提升下游任务（如分类、聚类）的性能。

  • 方法：

    • 统计流形提供了一个更适合数据分布的测地线结构。
    • 通过优化潜在空间，使得 欧几里得直线能更好地近似测地线，从而减少潜在空间中的几何失真（Distortion Minimization）。

  • 结果：

    • 这种方法提供了更好的数据表征，使得线性分类器（如 SVM）可以更高效地分离数据，提高分类准确率。

举例：

  • 设想你有一组 3D 物体（比如猫、狗、马的点云），直接使用欧几里得空间可能会导致这些类别的分布是非线性的，难以用线性分类器（如 SVM）进行区分。
  • 但如果我们用统计流形学习到一个最佳的潜在表示，数据在潜在空间中可以变得更加线性分布，使得简单的线性分类器就可以实现更好的分类效果。

总结

  • 给点云提供了一种非欧的几何结构，能够更好地描述点云的形状和结构
  • 第一种应用主要用于形状变形（Morphing），通过测地线插值实现更加平滑的形变
  • 第二种应用主要用于数据表示学习（Representation Learning），优化潜在空间的坐标，使得数据分布更加线性，便于分类和分析

为什么统计流形的潜在空间能变得更加线性？

  • 统计流形的核心思想是用合适的几何结构来描述数据的分布。

  • 在统计流形中，点云数据可以被映射到一个更适合它们本质结构的空间，这样原本弯曲的数据分布可以被展开，使得它们在新的坐标系中更接近线性分布。

  • 直观理解：

    统计流形就像是一个数据的“展开地图”，它让数据按照其本质结构分布，使得线性方法（如 SVM）在该空间中更加有效。

如何理解低维的潜空间中的低维和潜空间

  • [x] 【低维】

  • 一个1000个点的点云，有(x,y,z)那么就可以用3000个参数来表示这个点云，但是我们可以找到一个更紧凑的表示，例如用10维向量来表示整个点云，而不是所有点的3D坐标

  • [x] 【潜空间】

  • 潜空间（Latent Space） 指的是一个通过学习获得的隐含数据表示空间，它是从原始高维数据中提取出来的一个新的、更有意义的空间。

  • 特点：

    • 保留核心信息，点云的几何结构
    • 维度低，计算高效
    • 几何结构可以优化，数据关系更加直观

2. Statistical Manifold Framework for Point Cloud Data

“A statistical manifold is an infinite-dimensional Riemannian manifold each of whose points is a probability density, with the Fisher information metric acting as a natural Riemannian metric.”

  • [x] 统计流形

  • 统计流形是一种黎曼流形（Riemannian Manifold），但它的每个点不是普通的数值点，而是一个概率密度函数（Probability Density Function, PDF）。

  • 这个流形是无穷维的（Infinite-Dimensional），因为概率密度函数可以是无穷维的（比如连续分布）。

  • 在这个流形上，我们使用 Fisher 信息度量 来定义几何距离，它是统计流形上的自然黎曼度量（Riemannian Metric）。

基本结构


S=\{p(x;\Theta)\mid \Theta\in\mathbb{R}^m\}

其中

  • \Theta=(\theta^1,\cdots,\theta^m)是概率分布的参数（均值协方差）

  • p(x;\Theta)是概率密度函数（高斯分布或者GMM）

  • [x] Fisher信息度量g_{ij}\Theta


g_{ij}(\Theta) = \int p(x; \Theta) \frac{\partial \log p(x; \Theta)}{\partial \theta^i} \frac{\partial \log p(x; \Theta)}{\partial \theta^j} dx
  • Fisher-Rao距离D_{FR}

D_{FR}(p_1, p_2) = \sqrt{ (\mu_1 - \mu_2)^T \Sigma^{-1} (\mu_1 - \mu_2) + \text{Tr} \left( \Sigma^{-1} \Sigma_1 + \Sigma^{-1} \Sigma_2 - 2 \sqrt{\Sigma^{-1} \Sigma_1 \Sigma^{-1} \Sigma_2} \right)}
公式 作用 直观理解
Fisher 信息度量 g_{ij}(\Theta) 定义统计流形的局部几何结构 刻画流形上小范围内的度量，决定“微小变化的影响”
Fisher-Rao 距离 D_{FR} 计算统计流形上两个点（两个概率分布）之间的全局距离 刻画两个概率分布之间的“测地线距离”

难点在于Fisher信息度量，主要是定义局部几何结构，决定了这个曲面的度量单位

我的理解：

度量这个东西就好像我们北京和新加坡在地图上各往东走1cm，但是实际上是不一样的，所以g_{ij}更描述的是局部的概念，例如下面的计算测地线的公式是对于g_{ij}逐步积分

  • 经典测地线计算 需要先求出 Fisher 信息度量 g_{ij}(\Theta)，然后通过求解测地线方程得到 Fisher-Rao 距离： 

D_{FR}(p_1, p_2) = \int_0^1 \sqrt{g_{ij}(\theta) d\theta^i d\theta^j}
  • 对于高斯分布，Fisher 信息度量是固定的，可以直接写出 Fisher-Rao 距离的封闭解，这使得我们计算 D_{FR} 时 不需要再显式求解测地线。

我的理解：

如果是更复杂的分布（如 Dirichlet 分布、指数族分布），那么就需要使用g_{ij}进行测地线地计算；而Fisher信息度量对于高斯分布是固定的，测地线具有解析解，可以直接使用封闭形式的公式。

  • 高斯分布 = 直线高速公路 🚗💨 → 你直接开车从 A 到 B，不需要考虑地形（测地线已知）。

  • 非高斯分布 = 翻山越岭 🏔️🥾 → 你必须计算地形的起伏g_{ij}，然后一步一步找最短路径。

2.1 Statistical Manifold of Point Cloud Data

关键点

点云数据\mathbf{X} = \{x_1, x_2, ..., x_n\}不是单纯的一组离散点，而是用概率密度函数p(x;\mathbf{X})表示

论文采用的核密度估计（Kernel Density Estimation, KDE）方法，即用一个平滑核函数K(u)进行估计。这样可以让点云数据在统计流形上有连续表示（存疑）

定义2.2： 核密度估计公式

核密度估计（KDE）用于从离散点云数据 \mathbf{X} 估计出平滑的概率密度函数：


p(x; \mathbf{X}) := \frac{1}{n \sqrt{|\Sigma|}} \sum_{i=1}^{n} K\left(\Sigma^{-\frac{1}{2}}(x - x_i) \right)
  • p(x; \mathbf{X})：点云数据\mathbf{X}生成的概率密度估计
  • K(\cdot)：核函数，例如高斯核，用于平滑估计点云分布
  • n：点云数
  • \Sigma：带宽矩阵，控制核函数的尺度
  • \Sigma^{-\frac{1}{2}}(x - x_i)对数据点进行带宽缩放，使得核函数在不同尺度上适用。

定义2.3 ：点云作为流形

点云\mathbf{X}形成一个流形，维度是nD，要求所有点不同

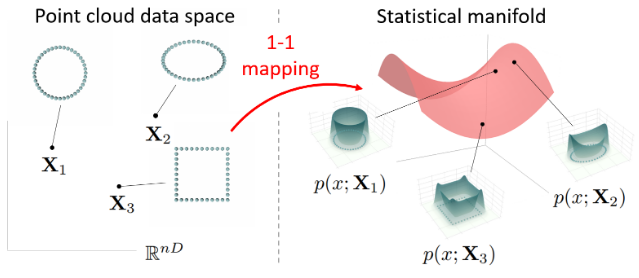
定义2.4：h(X)的1-1映射（需要一个严格正定的核函数）

点云流形\mathcal{X}到统计流形\mathcal{S}的映射h(\mathbf{X})是1-1对应的，需要一个严格正定的核函数


\Psi(x, y) = K\left(\Sigma^{-\frac{1}{2}}(x - y) \right)

需要选择合适的核函数（严格正定）

这保证了点云流形和统计流形之间的映射不会出现“不同的点云映射到相同的概率密度函数”

论文选择的核函数K(u)

使用的标准正态核（Gaussian Kernel）：


K(u) = \frac{1}{\sqrt{(2\pi)^D}} \exp\left(-\frac{u^T u}{2}\right)

2.2 信息黎曼度量

这里引入了Fisher信息度量，其被用于点云数据的统计流形\mathcal{S}赋予黎曼度量

这个度量定义了点云数据流形的几何结构，使得我们可以计算点云之间的距离和角度

  • 点云的数据X是一个矩阵表示， X\in\mathbb{R}^{n\times D}

  • 矩阵的表示并不是唯一的，我们应用置换矩阵P（即改变点云的顺序），那么X和PX仍然表示相同的点云。

  • 点云的的顺序不应该概率密度的工具，p(x;X)=p(x;PX)对任何置换矩阵p都成立

  • 这里也有局部坐标和切平面，点云\mathbf{X}在局部坐标系中的表示是\mathbf{X}\in\mathbb{R}^{n\times D}，切向量\mathbf{V}\in T_{\mathbf{X}}\mathcal{X}

信息黎曼度量的局部坐标表示


H_{ijkl}(X) := \int p(x; X) \frac{\partial \log p(x; X)}{\partial X^{ij}} \frac{\partial \log p(x; X)}{\partial X^{kl}} dx

  • H_{ijkl}(X) 是 信息黎曼度量 在局部坐标系中的表达。

  • 这个度量通过对 概率密度函数的对数 进行求导计算，并且在每个坐标维度上进行积分。

  • 具体来说，度量矩阵 H_{ijkl}(X) 捕捉了点云在局部坐标上的几何结构，并且定义了切向量之间的内积。

  • 表达式是置换不变的，改变点云顺序不会影响结果

切向量的内积


\langle V, W \rangle_X := \sum_{i,k=1}^{n} \sum_{j,l=1}^{D} H_{ijkl}(X) V^{ij} W^{kl}

这个内积表示了两个切向量之间的角度和长度关系。（存疑）

信息黎曼度量的标准高斯核表达式


\int p(x; X) K\left( \frac{x - x_i}{\sigma} \right) K\left( \frac{x - x_k}{\sigma} \right) \left[ \frac{(x - x_i)(x - x_k)^T}{\sigma^4} \right] dx
  • 使用标准高斯核下信息黎曼度量的解析表达式
  • 带宽参数\sigma控制核函数的尺度
  • 表达式涉及到两点之间的相似度度量，即衡量点云中的两点在局部坐标系中的相关性

对于H(X)的理解

统计流形的维度是\mathbb{R}^{n\times D}，点云数据用矩阵存储，如：


X =
\begin{bmatrix}
x_1^{(1)} & x_1^{(2)} & \dots & x_1^{(D)} \\
x_2^{(1)} & x_2^{(2)} & \dots & x_2^{(D)} \\
\vdots & \vdots & \ddots & \vdots \\
x_n^{(1)} & x_n^{(2)} & \dots & x_n^{(D)}
\end{bmatrix}

其中x_i^{(j)}表示点云中的第i个点，在第j维的坐标值，H_{ijkl}(X)本质上是一个度量矩阵，它衡量：

  1. 第i,j维度上的变化对第k,l维度上的变化的影响
  2. 就像一个交叉相关性，表示不同坐标之间的相互作用

由于只有两个偏导数相乘，所以我们只需要两个变量X^{ij}和X^{kl}之间的关系

这里有点绕，但是我也稍微理解了，假设点云数据如


X=\begin{bmatrix} 1.0 & 2.0 \\ 2.5 & 3.0\\ 4.0 & 5.5
\end{bmatrix}

如果我们计算H_{1122}(X)表示第1个点的x轴坐标X^{11}和第2个点的y轴坐标X^{22}之间的相关性.如果这个值很大，表示二者之间关系大。

如何理解这个二者之间关系大？我们举个例子

  1. 两个橡皮筋A和B，我变化A，B不会变化，因为二者分离；如果A和B绑在一起，我变化A，那么B也会变化

  2. 那么为什么改变某个点的某个方向，会引起另外一个点的另外一个方向的改变呢？

    假设A(1,2)和B(4,3)，在这两个点处各有一个高斯分布，每个点产生一个高斯核，这两个叠加决定了整个平面上的概率密度分布

    那么此时A从(1,2)到(2,2)移动，整个KDE的形状变化，由于A的核影响(x,y)的概率密度p(x,y)，B处的p(x,y)也会发生变化，尤其是y方向的，因为概率密度 p(x,y)p(x, y)p(x,y) 在该方向上的梯度变得更大

ok，那么回顾一下fisher信息度量和这个H_{ijkl}有什么区别和联系？

fisher信息度量（基于分布参数的\theta）：


g_{ij}(\theta) = \int p(x; \theta) \frac{\partial \log p(x; \theta)}{\partial \theta^i} \frac{\partial \log p(x; \theta)}{\partial \theta^j} dx

信息黎曼度量（参数是点云数据X本身）：


H_{ijkl}(X) = \int p(x; X) \frac{\partial \log p(x; X)}{\partial X^{ij}} \frac{\partial \log p(x; X)}{\partial X^{kl}} dx

并且这个度量对于任何n\times n置换矩阵P，度量保持不变，不依赖点云的编号方式

速度矩阵的欧几里得范数与信息黎曼度量的关系

论文提到：

  • 在欧几里得度量下，两个点云数据的速度矩阵可能相同

  \Vert V\Vert^2=\sum_{i=1}^n\sum_{j=1}^DV^{ij}V^{ij}
  • 但在信息黎曼度量下，速度可以不同
    • 速度A为0.2626，意味着这个点云的运动在信息黎曼度量下有较大的影响
    • 速度B为2.2\times 10^{-8}，意味着这个点云的运动在信息黎曼度量下几乎没有影响
    • 比如速度A是真正改变点云形状的运动，比如改变了局部的几何结构，如图3
    • 而速度B是无关紧要的运动，例如刚性平移旋转，仅仅改变了点云的顺序，没有改变概率密度的形状
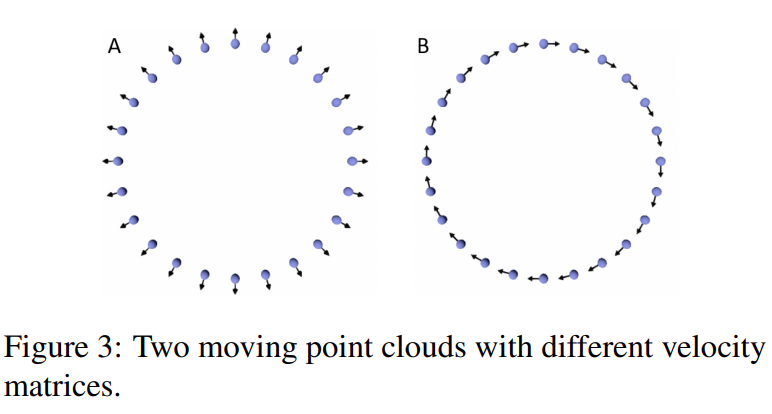
image-20250313141951244

因为欧式空间里面只看速度，不管其他的，而信息黎曼度量里面则依赖于H_{ijkl}(X)，而不是对所有坐标求平方和

H_{ijkl}(X) 衡量点云在统计流形上的几何结构，它告诉我们：

  • 哪些方向的变化是重要的，哪些是不重要的。
  • 刚性平移可能在这个度量下几乎不改变几何结构，所以速度接近 0。
  • 形状变形可能会显著改变密度估计，所以度量值较大。

可以稍微类比，我在游泳池里游泳

  • 我仅仅飘浮，水面无变化
  • 我用力拍打，形成了波浪，水面流动有很大的扰动

在这里：

  • 水的流动=点云的概率密度估计p(x;X)
  • 我的动作=点云数据的运动
  • 水波是否被扰动=H_{ijkl}(X)的影响程度

3. Applications to Point Cloud Autoencoders

点云自编码器。

论文提出通过信息黎曼度量，可以为解码流形定义一个合适的度量，使得

  1. 可以计算解码流形上的测地线（最短路径）
  2. 通过把数据空间的黎曼度量头应到这个流形上，可以得到一个更合理的几何度量

如何构造解码流形上的度量？

点云解码器：


f:\mathbb{R}^m\rightarrow \mathbb{R}^{n\times D}
  • \mathbb{R}^m是潜在空间低维表示
  • \mathbb{R}^{n\times D}是点云数据的高维表示
  • 解码器f将潜在表示映射回点云空间

论文给出的公式：


G_{ab}(z) := \sum_{i,k=1}^{n} \sum_{j,l=1}^{D} H_{ijkl}(f(z)) (J_f)_{a}^{ij} (J_f)_{b}^{kl}.

  • G_{ab}(z) 是解码流形上的度量张量（它在潜在空间 z 上定义）。

  • H_{ijkl}(f(z))是点云统计流形上的度量，在f(z) 处计算。

  • J_f 是解码器 f 的 Jacobian 矩阵，用于将度量从高维点云空间拉回到潜在空间。

为什么需要G(z)？

因为G_{ab}(z)是解码流形上的度量

  1. 测地线插值

    在潜在空间\mathbb{R}^m中，两个点云的潜在表示z_1和z_2的最短路径可以用测地线计算


   \min_{z(t)} \int_0^1 \dot{z}(t)^T G(z(t)) \dot{z}(t) dt.

  1. 优化潜在空间的坐标系

    通过最小化度量G_{ab}(z)的变形，可以让潜在空间的距离尽可能保持点云的几何关系

    这意味着在潜在空间上做简单的线性插值，也能很好地对应点云之间的测地线

我理解的：

首先我对于原始点云需要升维，对每个点云建立一些高斯分布模型，这个就是统计流形。然后，因为维度太高，我需要将其转化成低维的潜在空间，然后最后用解码器恢复回去。

一共四个空间

学习最优的潜在空间坐标（Learning Optimal Latent Space Coordinates）

我们需要学习更好的潜在空间坐标，利用信息黎曼度量G(z)来优化潜在空间的结构，使得潜在空间能够更好地保留几何信息（如距离和角度）。

因为点云数据的复杂性，潜在空间的度量G(z)可能是不规则的。论文希望让G(z)变得更贵则。

如何优化？

论文提出一个正则化项，让G(z)尽可能接近一个常数倍的单位矩阵，即cI


G(z)=cI

如果 G(z) 是 cI，那么潜在空间中的欧几里得距离就可以很好地近似测地线距离。

为什么呢？

测地线公式：


\min_{z(t)} \int_0^1 \dot{z}(t)^T G(z(t)) \dot{z}(t) dt.

代入得到：


\begin{aligned}
&\min_{z(t)} \int_0^1 \dot{z}(t)^T cI \dot{z}(t) dt\\
=&\min_{z(t)} \int_0^1 c\Vert\dot{z}(t)\Vert^2 dt
\end{aligned}
  • 这是 普通欧几里得空间中的最短路径问题！
  • 最优解是直线z(t) = (1-t) z_1 + t z_2
  • 也就是说，测地线在这个情况下就是欧几里得直线

直观理解：

可以把 G(z) 想象成 空间中的测量尺：

  • 如果 G(z) 变化不均匀（比如某些方向测量尺度大，某些方向测量尺度小），那么最短路径可能是弯曲的。
  • 如果 G(z) 是 cI，表示所有方向上的测量尺度是相同的，相当于使用了一把均匀的测量尺，这样测地线就变成普通的欧几里得直线。

论文才用一个正则化计数，用于优化G(z)，正则化损失为：


\mathbb{E}_{z \sim P} \big[ \| G(z) - cI \|_F^2 \big].

使用了一种mix-up风格的采样策略


z=\alpha z_1+(1-\alpha)z_2

mix-up采样

不拘于z_1,z_2，\alpha \sim U(-\eta, 1+\eta)是从一个均匀分布U采样的随机系数，这里\eta \gt 0

例如z_1=(0.2,0.5), z_2=(0.8,0.3)两个点云的潜在表示，如果直接训练只会对于z_1,z_2有用，但是此时取\alpha=0.7，新的变量z=\alpha z_1+(1-\alpha)z_2=0.7(0.2,0.5)+0.3(0.8,0.3)=(0.38,0.44)，新的训练样本

对于G(z)的一些思考

  • 和H(X)的区别？

    区别在于G(z)针对于潜在空间，而H(X)针对于统计流形的高维空间

  • G(z)是否是固定的，可以学习吗？
    可以学习。对于公式


  G_{ab}(z) := \sum_{i,k=1}^{n} \sum_{j,l=1}^{D} H_{ijkl}(\textcolor{red}{f(z)}) (J_f)_{a}^{ij} (J_f)_{b}^{kl}

潜在空间度量G(z)由统计流形度量H(X)通过解码器f(z)的JacobianJ_f传递得到的，最主要的是J_f由解码器f(z)决定，而f(z)是一个神经网络，被训练得到

4. 实验结果 Experimental Results

（懒得写了，具体看论文吧，感觉主要是插值）

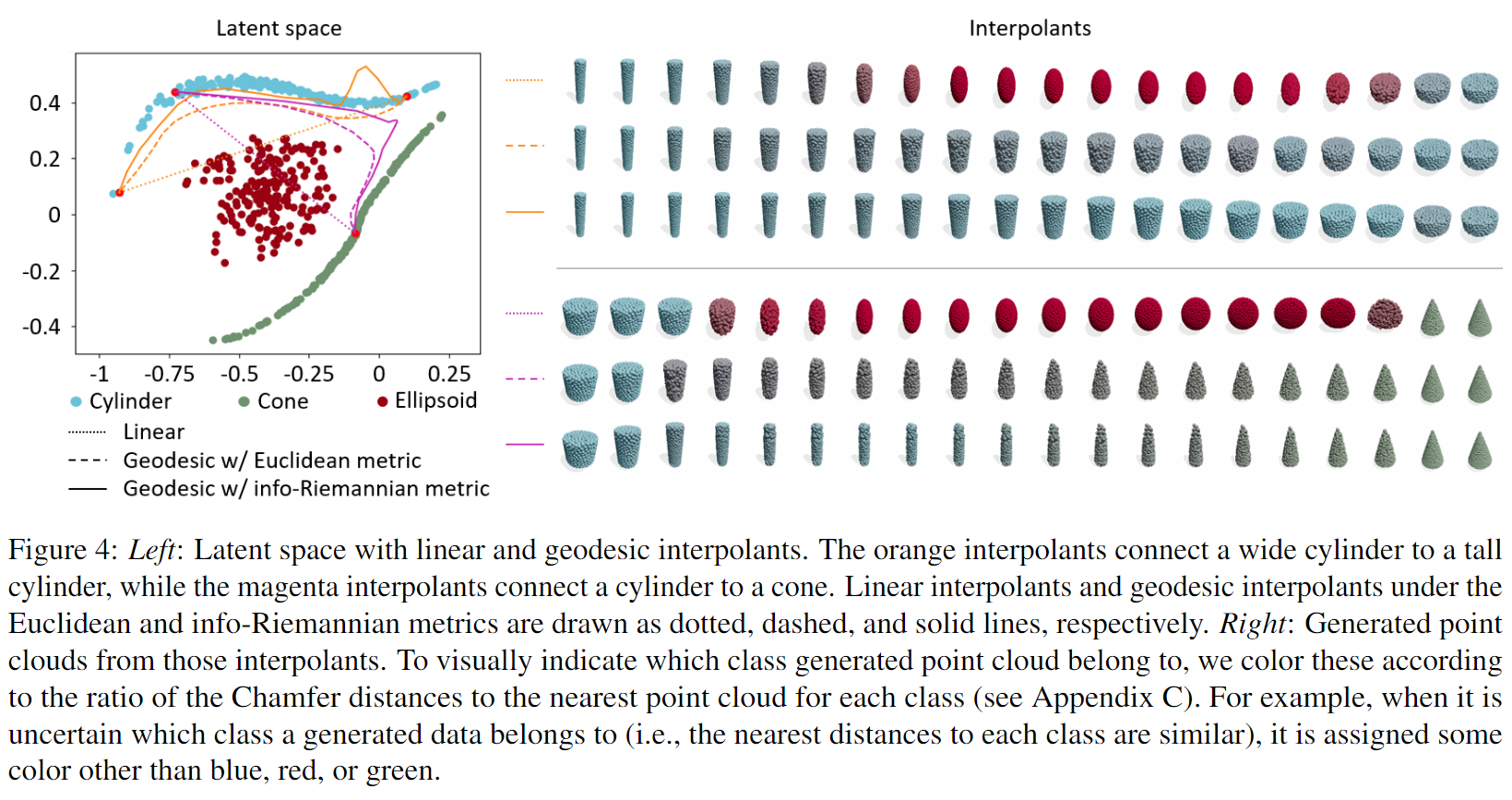
image-20250313155147576

左侧（Latent Space Visualization）：

  • 展示了潜在空间（Latent Space）中的形状分布（圆柱、圆锥、椭球）。
  • 黑色实线（Geodesic w/ Info-Riemannian metric）：信息黎曼度量下的测地线插值。
  • 黑色虚线（Geodesic w/ Euclidean metric）：欧几里得度量下的测地线插值。
  • 黑色点线（Linear interpolation）：潜在空间中的线性插值路径。

右侧（Generated Interpolants）：

  • 展示了从潜在空间插值点生成的点云形状。
  • 颜色表示形状类别
    • 蓝色（Cylinder）
    • 绿色（Cone）
    • 红色（Ellipsoid）
    • 灰色（不确定类别，混合形状）

关键观察点：

  1. 信息黎曼度量的测地线更合理：
    • 在 信息黎曼度量下（黑色实线），插值路径保持在同类别区域内，避免了跨类别的形状突变。
    • 在 欧几里得度量下（黑色虚线），插值路径可能会穿越错误类别区域（例如从圆柱变成椭球）。
  2. 点云插值的形状稳定性：
    • 使用欧几里得度量的插值（下方） 生成了许多混合形状（灰色），显示类别不稳定。
    • 使用信息黎曼度量的插值（上方），插值点云大多保持在相同类别（圆柱 → 圆柱，圆锥 → 圆锥）。

图4没有加正则化，图5加了正则化

在 Figure 5 里，经过正则化，类别边界更加清晰，插值路径更加稳定。

形状类别（如圆柱、圆锥、椭球）被更好地分离，减少了错误类别的插值。

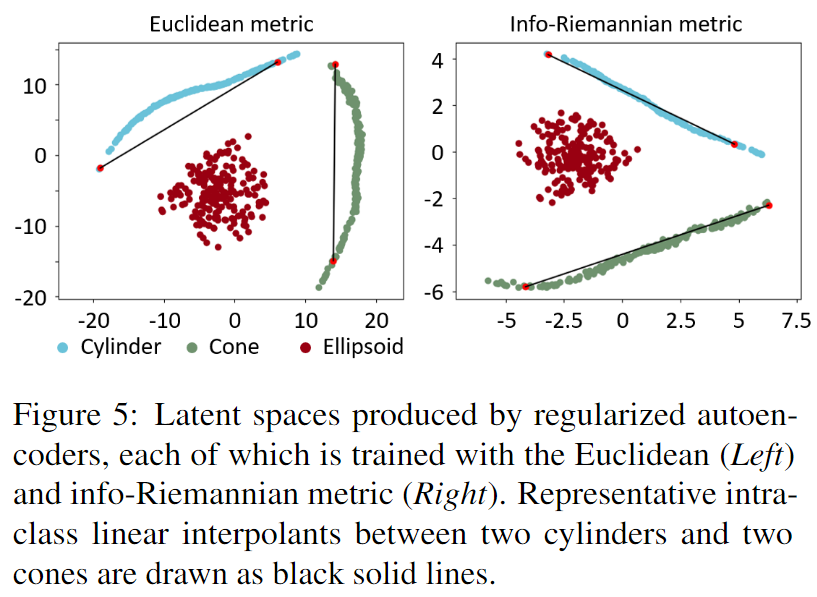
image-20250313155429891

对比使用正则化后的潜在空间（右）与未正则化的潜在空间（左，Figure 4）

观察点：

  1. 潜在空间更加规则
    • 经过正则化后，椭球和圆锥的类别分布更加分离，减少了类别混杂的情况。
  2. 插值路径更稳定
    • 在信息黎曼度量的正则化潜在空间中，插值路径更加平滑，不会轻易跨类别。
  3. 类内插值效果更好
    • 在 信息黎曼度量下，类内插值（如圆柱到圆柱）保持形状类别一致，而欧几里得度量可能会产生中间形状的突变。
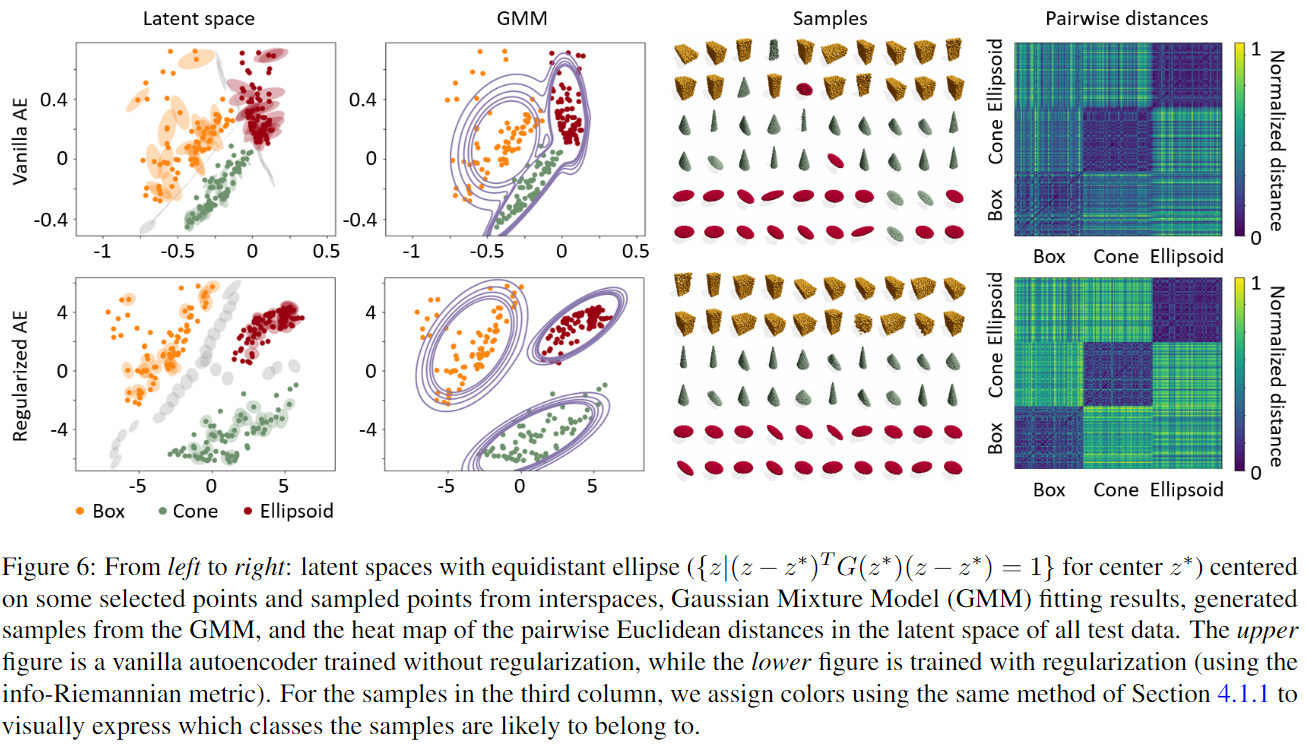
image-20250313155604184
  • 第一列
    • 上面是：普通自编码器。（类别边界模糊）
    • 下面是：正则化自编码器（边界增大，更清晰）
  • 第二列
    • 高斯混合模型（GMM）对潜在空间进行拟合，展示聚类情况
    • 正则化之后类别干扰更小
  • 第三列
    • 上面是普通自编码器，生成点云形状比较模糊
    • 下面是正则化自编码器，更加清楚，类别一致
  • 第四列
    • 计算潜在空间中不同点之间的欧几里得举例，显示形状类别的可分性
    • 正则化后，不同类别的的距离增大，表示类别区分度提高

这里展示了正则化的作用，以后做东西的时候多考虑一下正则化。对正则化也需要更多的研究。

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注