迭代求解线性方程组
这个问题主要是要求解线性方程组Ax=b问题,在本文都以如下求解如下方程组:
\underbrace{\begin{bmatrix}
3 & 1 & 1 \\
1 & 3 & 1 \\
1 & 1 & 3
\end{bmatrix}}_{A}
\underbrace{\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}}_{x}
=
\underbrace{\begin{bmatrix}
6 \\
3 \\
5
\end{bmatrix}}_{b}
首先可以这么理解,需要进行一个迭代的公式,然后找到一个合适的方法去逼近,那么肯定形如x_{k+1}=g(x_k),我们可以做得变换:x=x-C(Ax-b),其实也就是左右构造x并且关联一个稀疏C,那么我们需要得到一个合适矩阵C即可求解。
当然,如果C=A^{-1}的时候,就是最优的时候,因为直接可以得到x=A^{-1}b,这当然是不现实的。那么就需要找到一个合适的方法去逼近,这就有如下的Jacobi等一系列方法
Jacobi迭代法
首先需要介绍什么是严格对角占优矩阵,即对角线上的每个位置都比同行其他所有的值都大,这样可以认为对角元素占据A的主导作用,可以用对角元素组成对角阵近似A:
A\approx D=\text{diag}(A)
即:
A = \begin{bmatrix}
\textcolor{red}{a_{11}} & a_{12} & \cdots & a_{1n} \\
a_{21} & \textcolor{red}{a_{22}} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & \textcolor{red}{a_{nn}}
\end{bmatrix}
\approx
\begin{bmatrix}
\textcolor{red}{a_{11}} & 0 & \cdots & 0 \\
0 & \textcolor{red}{a_{22}} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \textcolor{red}{a_{nn}}
\end{bmatrix}
= D
如果是这样的话,我们可以用主对角线组成的对角矩阵D来近似原来的A,也就是C=D^{-1}去代替迭代公式。同时我们将矩阵A拆分成三个矩阵:上三角矩阵U、下三角矩阵L和对角矩阵D,有A=D+L+U,即:
A = \underbrace{\begin{bmatrix}
a_{11} & 0 & \cdots & 0 \\
0 & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn}
\end{bmatrix}}_D
+
\underbrace{\begin{bmatrix}
0 & 0 & \cdots & 0 \\
a_{21} & 0 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n(n-1)} & \cdots & 0
\end{bmatrix}}_L
+
\underbrace{\begin{bmatrix}
0 & a_{12} & \cdots & a_{1n} \\
0 & 0 & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0
\end{bmatrix}}_U
此时用C=D^{-1}代入迭代公式,有:
\begin{align}
x&=(I-CA)x+Cb\\
&=(I-D^{-1}(D+L+U))x+D^{-1}b\\
&=-D^{-1}(L+U)x+D^{-1}b
\end{align}
其实也可以直接拆分而来,即:
\begin{align}
Ax&=b\\
(D+L+U)x&=b\\
D&x=-(L+U)x+b\\
x&=-D^{-1}(L+U)x+D^{-1}b
\end{align}
那么就可以有迭代公式:
x^{(k+1)}=-D^{-1}(L+U)x^{(k)}+D^{-1}b
OK,至此写到这差不多完整了,但是看起来有这么多矩阵看起来云里雾里的,那么就开始拆分举例一下,首先D^{-1}并不难计算,例如我随便写一个
D^{-1}=\begin{bmatrix}
3 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 4
\end{bmatrix}^{-1}=\begin{bmatrix}
\frac{1}{3} & 0 & 0 \\
0 & \frac{1}{2} & 0 \\
0 & 0 & \frac{1}{4}
\end{bmatrix}
那再可观一些,看一开始说的矩阵可以写成我们中学阶段如下的方式:
\begin{cases}
3u+v+w=6\\
u+3v+w=3\\
u+v+3w=5
\end{cases}
\Rightarrow
\begin{cases}
u=\dfrac{6-v-w}{3}\\
v=\dfrac{3-u-w}{3}\\
w=\dfrac{5-u-v}{3}
\end{cases}
在求解u的时候,需要知道v,w就可以求出,那么我们根据上一个的解来计算新的u即可,其他同理。那么这个跟矩阵有什么关系呢?
我将迭代公式写成如下形式:
\begin{align}
x^{(k+1)}&=-D^{-1}(L+U)x^{(k)}+D^{-1}b\\
&=D^{-1}(b-(L+U)x)
\end{align}
以及开始有相似之处了,其实D^{-1}就是分母,也就是主对角线对应自己元素的倒数,那(L+U)的意义是什么呢?实际上就是除开自己的其他所有的值,即b-(L+U)x对应的就是6-(1\times v+1\times w)
至此,每次使用之前的值来迭代生成新的值就会一直接近,当然,这里没有将收敛条件,这里还有一个问题,为什么可以这样?或者说一定要主对角线严格占优吗?
不,Jacobi迭代法不一定要求矩阵严格对角占优,但在严格对角占优或正定的情况下,它的收敛性可以得到保证。
Gauss-Seidel迭代
在这之前讲了那么多的Jacobi迭代法是有原因的,因为GS迭代法在这上面加了一点点的小改动,我们观测到:
\begin{cases}
\textcolor{red}{u^{(k+1)}}=\dfrac{6-v^{(k)}-w^{(k)}}{3}\\
\textcolor{blue}{v^{(k+1)}}=\dfrac{3-\textcolor{red}{u^{(k)}}-w^{(k)}}{3}\\
w^{(k+1)}=\dfrac{5-\textcolor{red}{u^{(k)}}-\textcolor{blue}{v^{(k)}}}{3}
\end{cases}
我们在Jacobi迭代法中首先通过上一步的v^{(k)}和w^{(k)}计算的是u^{(k+1)},然后用上一步的u^{(k)}和w^{(k)}计算v^{(k+1)},那么在此时是不是发现我现在已经得到了比u^{(k)}更近似的解u^{(k+1)}呢?那么我可以用上一步的直接作用在此时,即:
\begin{cases}
\textcolor{red}{u^{(k+1)}}=\dfrac{6-v^{(k)}-w^{(k)}}{3}\\
\textcolor{blue}{v^{(k+1)}}=\dfrac{3-\textcolor{red}{u^{(k+1)}}-w^{(k)}}{3}\\
w^{(k+1)}=\dfrac{5-\textcolor{red}{u^{(k+1)}}-\textcolor{blue}{v^{(k+1)}}}{3}
\end{cases}
那么此时的迭代法是什么样的呢?我们不将L移到右边,有
(D+L)x^{(k+1)}=b-Ux^{(k)}
这里可以看出右侧的b-Ux^{(k)}使用的是上一轮的x^{(k)},而对于已经获得的,就使用的是x^{(k+1)},例如此时是a_{22},那么a_{21}对应的系数乘以的应该是新的x^{(k+1)},而a_{23}乘以的就应该是上一轮的x^{(k)}。
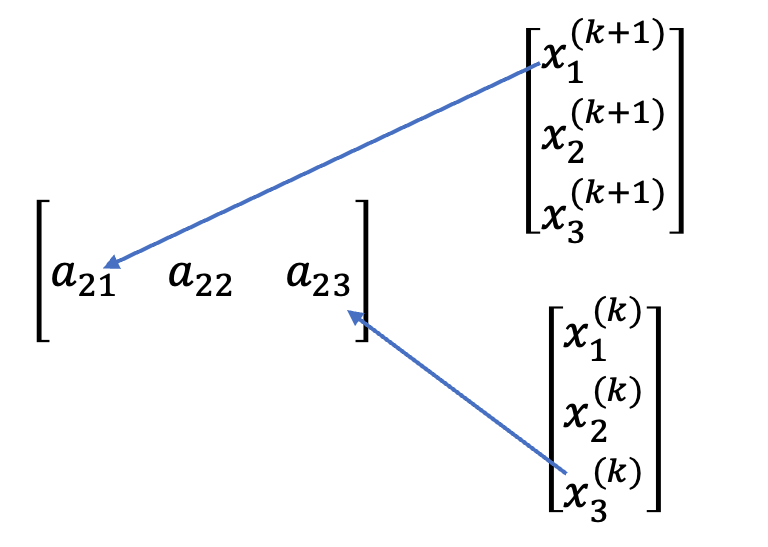
对于代码上也仅有一处不同:
for (int i = 0; i < n; i++) {
x1[i] = b[i];
for (int j = 0; j < n; j++) {
if (j < i) x1[i] -= A[i][j] * x1[j]; // 这里需要乘以已经有的x1[j]
else if (j > i) x1[i] -= A[i][j] * x0[j]; // 而Jacobi迭代法只有这一行
}
x1[i] /= A[i][i];
}梯度下降法-共轭梯度法
求解Ax=b问题上,共轭梯度法的目标是通过构造一系列方向,快速逼近线性方程组的解。并对每一步的方法做了特殊的设计,使得在更新时可以保证搜索方向的共轭性,从而更快地逼近。
考虑最小化二次函数,求解
f(\vec{x})\equiv \frac{1}{2}\vec{x}^\top Ax^\top -\vec{b}^\top \vec{x}+c
当A是对称的时候,有\nabla f(\vec{x})=A\vec{x}-\vec{b},当梯度为的时候,此时函数值最小的时候即是梯度为的时候,也就是A\vec{x}=\vec{b}的解,也就是只需要求解该函数最小值在哪里。
线搜法
迭代由下式给出
x_{k+1}=x_k+\alpha_kp_k
它的思想是选择一个初始位置x_0,每走一步使得函数值满足f(x_{k+1})\lt f(x_{k}),不同的方法选择搜索方向p_k和步长\alpha_k,步长决定了应该在p_k方向上前进的距离,即最小化下面的函数
\phi(\alpha)=f(x^{(k)}+\alpha p^{(k)})
目标是找到使得\phi(\alpha)最小的\alpha,即:
\alpha_k=\arg \min_\alpha \phi(\alpha)
其实此时就是选择当前位置的负梯度的方向,可以理解为负导数的方向,有:
\begin{align}
\mathbf{p}^{(k)} &= - \nabla f(\mathbf{x}^{(k)}) = \mathbf{b} - A \mathbf{x}^{(k)}
\\
\mathbf{x}^{(k+1)} &= \mathbf{x}^{(k)} + \alpha_k (\mathbf{b} - A \mathbf{x}^{(k)})
\end{align}
要找到最优步长\alpha_k,需要最小化函数f(\mathbf{x}^{(k)} + \alpha \mathbf{p}^{(k)})
f(\mathbf{x}^{(k)} + \alpha \mathbf{p}^{(k)}) = \frac{1}{2} (\mathbf{x}^{(k)} + \alpha \mathbf{p}^{(k)})^T A (\mathbf{x}^{(k)} + \alpha \mathbf{p}^{(k)}) - \mathbf{b}^T (\mathbf{x}^{(k)} + \alpha \mathbf{p}^{(k)}) + c
接下来需要对\alpha求导得到:
\frac{d}{d\alpha} f(\mathbf{x}^{(k)} + \alpha \mathbf{p}^{(k)}) = 0
展开得到最后的步长公式:
\alpha_k = \frac{\mathbf{r}_k^T \mathbf{r}_k}{\mathbf{p}_k^T A \mathbf{p}_k}
其中:
\mathbf{r}_k = \mathbf{b} - A \mathbf{x}^{(k)},是第k步的残差\mathbf{p}_k是搜索方向,是负梯度方向
共轭梯度法
共轭梯度法与梯度下降法的相似点在于它也会每次选择一个方向来前进,但它的选择方向更加高效。共轭梯度法不再每一步简单地沿着负梯度方向前进,而是沿着共轭方向前进。
什么是共轭方向?
两个方向
\mathbf{p}_i 和 \mathbf{p}_j对于矩阵 A 是共轭的,如果它们满足:
\mathbf{p}_i^T A \mathbf{p}_j = 0 \quad \ i \neq j
共轭梯度法能构造出一系列的共轭方向,保证每一步的搜索不会重复之前的计算路径,从而更快的收敛。
步骤如下:
- 初始设置
选择初始解 \mathbf{x}^{(0)} ,计算初始残差 \mathbf{r}^{(0)} = \mathbf{b} - A \mathbf{x}^{(0)} ,并将初始搜索方向设为残差: \mathbf{p}^{(0)} = \mathbf{r}^{(0)} 。
- 计算步长
仍然需要一个步长前进
\alpha_k = \frac{\mathbf{r}^{(k)^T} \mathbf{r}^{(k)}}{\mathbf{p}^{(k)^T} A \mathbf{p}^{(k)}}
- 更新解
x^{(k+1)}
\mathbf{x}^{(k+1)} = \mathbf{x}^{(k)} + \alpha_k \mathbf{p}^{(k)}
- 更新残差
\mathbf{r}^{(k+1)}
\mathbf{r}^{(k+1)} = \mathbf{r}^{(k)} - \alpha_k A \mathbf{p}^{(k)}
- 计算方向更新稀疏
\beta_k
\beta_k = \frac{\mathbf{r}^{(k+1)^T} \mathbf{r}^{(k+1)}}{\mathbf{r}^{(k)^T} \mathbf{r}^{(k)}}
- 更新搜索方向
\mathbf{p}^{(k+1)}
\mathbf{p}^{(k+1)} = \mathbf{r}^{(k+1)} + \beta_k \mathbf{p}^{(k)}
- 迭代,直到满足条件
共轭梯度法则通过保证搜索方向的共轭性,避免了重复搜索,确保每一步的前进都是独立的、有效的。
代码与结果
#include <iostream>
#include <cmath>
#include <fstream>
#define double long double
#define sqr(x) ((x) * (x))
#define eps 1e-3
using namespace std;
int max_iter = 30;
double calcMSE(const vector<double> &x0, const vector<double> &x1) {
double mse = 0.0;
for (int i = 0; i < x0.size(); i++) {
mse += sqr(x0[i] - x1[i]);
}
return mse / x0.size();
}
void readMatrix(vector<vector<double>> &A, vector<double> &b) {
freopen("input.txt", "r", stdin);
int n;
cin >> n;
A.assign(n, vector<double>(n, 0.0));
b.assign(n, 0.0);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> A[i][j];
}
}
for (int i = 0; i < n; i++) {
cin >> b[i];
}
}
void Jacobi(const vector<vector<double>> &A, const vector<double> &b, int max_iter) {
int n = A.size();
vector<double> x0(n, 0.0), x1(n, 0.0);
int iter = 0;
double mse = 1;
while (iter < max_iter && mse > eps) {
iter++;
for (int i = 0; i < n; i++) {
x0[i] = x1[i];
}
for (int i = 0; i < n; i++) {
x1[i] = b[i];
for (int j = 0; j < n; j++) {
if (j i) continue;
x1[i] -= A[i][j] * x0[j];
}
x1[i] /= A[i][i];
}
mse = calcMSE(x0, x1);
}
cout << "Jacobi迭代法结果:" << endl;
for (int i = 0; i < n; i++) {
cout << "x[" << i << "] = " << fixed << setprecision(6) << x1[i] << endl;
}
cout << "迭代次数:" << iter << endl;
cout << "均方误差:" << fixed << setprecision(6) << mse << endl;
}
void GaussSeidel(const vector<vector<double>> &A, const vector<double> &b, int max_iter) {
int n = A.size();
vector<double> x0(n, 0.0), x1(n, 0.0);
int iter = 0;
double mse = 1;
while (iter < max_iter && mse > eps) {
iter++;
for (int i = 0; i < n; i++) {
x0[i] = x1[i];
}
for (int i = 0; i < n; i++) {
x1[i] = b[i];
for (int j = 0; j < n; j++) {
if (j < i) x1[i] -= A[i][j] * x1[j];
else if (j > i) x1[i] -= A[i][j] * x0[j];
}
x1[i] /= A[i][i];
}
mse = calcMSE(x0, x1);
}
cout << "Gauss-Seidel迭代法结果:" << endl;
for (int i = 0; i < n; i++) {
cout << "x[" << i << "] = " << fixed << setprecision(6) << x1[i] << endl;
}
cout << "迭代次数:" << iter << endl;
cout << "均方误差:" << fixed << setprecision(6) << mse << endl;
}
void ConjugateGradient(const vector<vector<double>> &A, const vector<double> &b, int max_iter) {
int n = A.size();
vector<double> x0(n, 0.0), x1(n, 0.0), r0(n, 0.0), r1(n, 0.0), p0(n, 0.0), p1(n, 0.0);
double alpha, beta, mse = 1;
int iter = 0;
for (int i = 0; i < n; i++) {
r0[i] = b[i];
for (int j = 0; j < n; j++) {
r0[i] -= A[i][j] * x0[j];
}
p0[i] = r0[i];
}
while (iter < max_iter && mse > eps) {
iter++;
alpha = beta = 0;
for (int i = 0; i < n; i++) {
alpha += r0[i] * r0[i];
} // alpha = r^T * r ([1])
vector<double> Ap(n, 0.0);
double res = 0, den = alpha;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
Ap[i] += A[i][j] * p0[j];
}
} // Ap = A * p ([n, 1])
for (int i = 0; i < n; i++) {
res += p0[i] * Ap[i];
} // res = p^T * A * p ([1])
alpha /= res; // alpha = r^T * r / p^T * A * p ([1])
for (int i = 0; i < n; i++) {
x1[i] = x0[i] + alpha * p0[i];
}
for (int i = 0; i < n; i++) {
r1[i] = r0[i] - alpha * Ap[i];
}
beta = 0;
for (int i = 0; i < n; i++) {
beta += r1[i] * r1[i];
} // beta = r^T * r ([1])
beta /= den; // beta = r^T * r / r0^T * r0 ([1])
for (int i = 0; i < n; i++) {
p1[i] = r1[i] + beta * p0[i];
}
mse = calcMSE(x0, x1);
x0 = x1;
r0 = r1;
p0 = p1;
}
cout << "共轭梯度法结果:" << std::endl;
cout << "迭代次数:" << iter << std::endl;
cout << "解向量:" << std::endl;
for (int i = 0; i < n; ++i) {
cout << "x[" << i << "] = " << std::fixed << std::setprecision(6) << x1[i] << std::endl;
}
cout << "最终残差:" << mse << std::endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
vector<vector<double>> A;
vector<double> b;
readMatrix(A, b);
Jacobi(A, b, max_iter);
GaussSeidel(A, b, max_iter);
ConjugateGradient(A, b, max_iter);
}第一个求解矩阵:
\begin{bmatrix}
1 & -1 & 0 \\
-1 & 2 & 1 \\
0 & 1 & 2
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}
=
\begin{bmatrix}
0 \\
2 \\
3
\end{bmatrix}
输出如下:
Jacobi迭代法结果:
x[0] = 0.968324
x[1] = 1.000000
x[2] = 1.015838
迭代次数:25
均方误差:0.000753
Gauss-Seidel迭代法结果:
x[0] = 1.000000
x[1] = 1.000000
x[2] = 1.000000
迭代次数:3
均方误差:0.000000
共轭梯度法结果:
迭代次数:4
解向量:
x[0] = 1.000000
x[1] = 1.000000
x[2] = 1.000000
最终残差:0.000000第二个求解矩阵:
\begin{bmatrix}
3 & 1 & 1 \\
1 & 3 & 1 \\
1 & 1 & 3
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix}
=
\begin{bmatrix}
6 \\
3 \\
5
\end{bmatrix}
输出如下:
Jacobi迭代法结果:
x[0] = 1.610787
x[1] = 0.110795
x[2] = 1.110789
迭代次数:11
均方误差:0.000728
Gauss-Seidel迭代法结果:
x[0] = 1.595234
x[1] = 0.101136
x[2] = 1.101210
迭代次数:4
均方误差:0.000096
共轭梯度法结果:
迭代次数:3
解向量:
x[0] = 1.600000
x[1] = 0.100000
x[2] = 1.100000
最终残差:0.000000