比赛链接:"蔚来杯"2022牛客暑期多校训练营1
今天是第一场多校,做的贼烂...演了队友一把,没读好题..希望明天的hdu多校加油!
G.Lexicographical Maximum(签到)
题意:给你一个数字$n(1\leq n\leq 10^{1000000})$,求小于$n$的最大子序列。
(PS:998>99,9>89)
思路:尽量凑9,如果是中间中断的话,例如989,那还不如99的,所以我们判断除了最后一位,前面的n-1位是否都是9,如果是的话则输出原来的(这时候肯定最大);否则输出n-1位的9。
代码:
inline void Case_Test()
{
cin>>s;
n = s.size();
bool ok = true;
for (int i=0;i<n-2;i++)
if (s[i]!='9')
ok=false;//ok = false 代表前面没有全是9
if (ok)
cout<<s;
else{
string ans(n-1,'9');//输出n-1个9
cout<<ans;
}
}
A.Villages: Landlines(贪心+排序)
题意:给你一个发电站以及n-1个建筑物,需要插入若干个变电塔使其传播电,给出$x_i,r_i$表示位置以及能够接收的范围...嗯题意我读了好久(不想说了..),求最小的代价能让这些连起来。
思路:实际上我可以插变电塔在区间的两端,这样别的链接的时候就只需要计算那个区间的左右区间即可,实际上可以转化成区间连起来需要多少代价。那就直接排序+贪心即可。
代码:
struct node
{
int l,r;
}a[N];
int x,d,n;
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>x>>d;
a[i].l = x-d;
a[i].r = x+d;
}
sort(a+1,a+1+n,[&](node &a,node &b){return a.l<b.l;});//对左边界排序,每次从左到右扫。
int r = a[1].r, ans = 0;
for (int i=2;i<=n;i++){
ans += Max(0,a[i].l-r);//大于0 才加上
r = Max(r,a[i].r);//当前的右边,每次拿这个比较
}
cout<<ans;
}
D.Mocha and Railgun(计算几何)
题意:给你一个中心为$(0,0)$半径为$r$的圆,你有一个长度为$2d$的线段,你可以让其按中间$(x,y)$旋转,让其左侧的圆弧在其的射影的弧长最大,求弧长。例如:
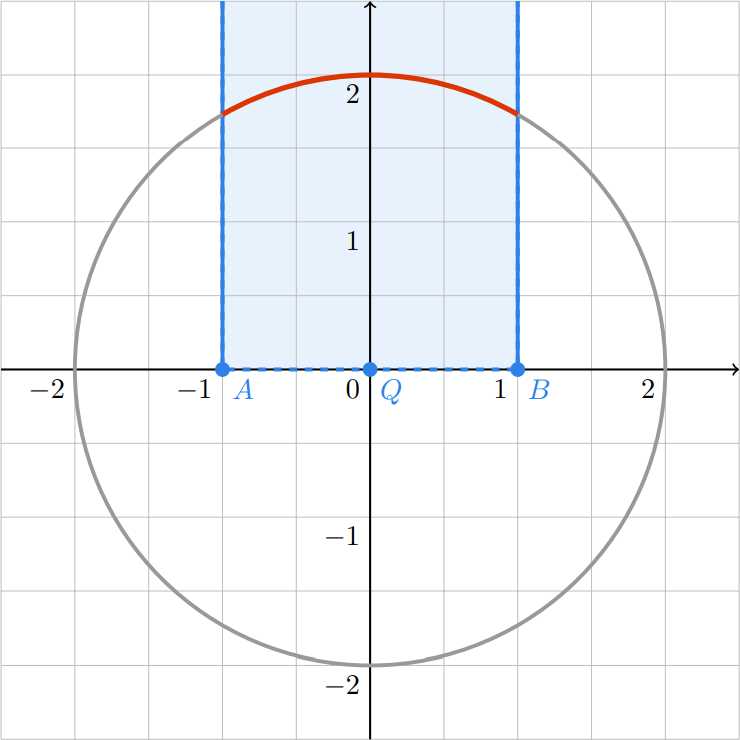
思路:让线段旋转延申成穿过圆心,也就是下图这样(这样可以使得线段越接近于“右边”),这样投影的弧长最大
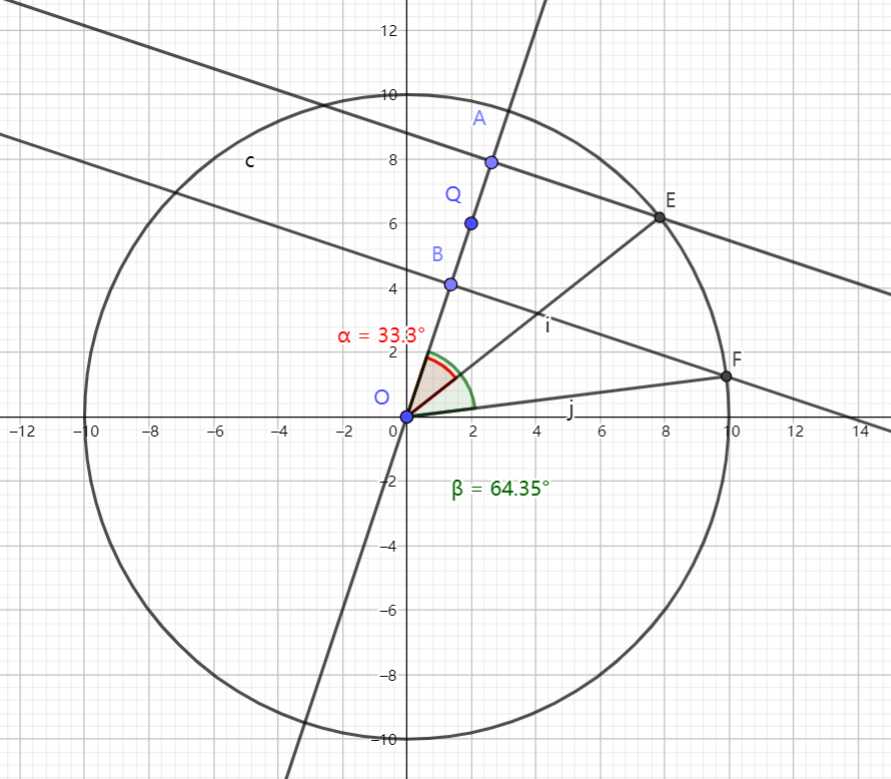
说的右边是什么意思呢,往右下旋转,这样摆的右边界越靠近右边,这样弧度变化最大。(这就是为什么题目说,线段距离圆C大于d,说明我这样一定在园内)
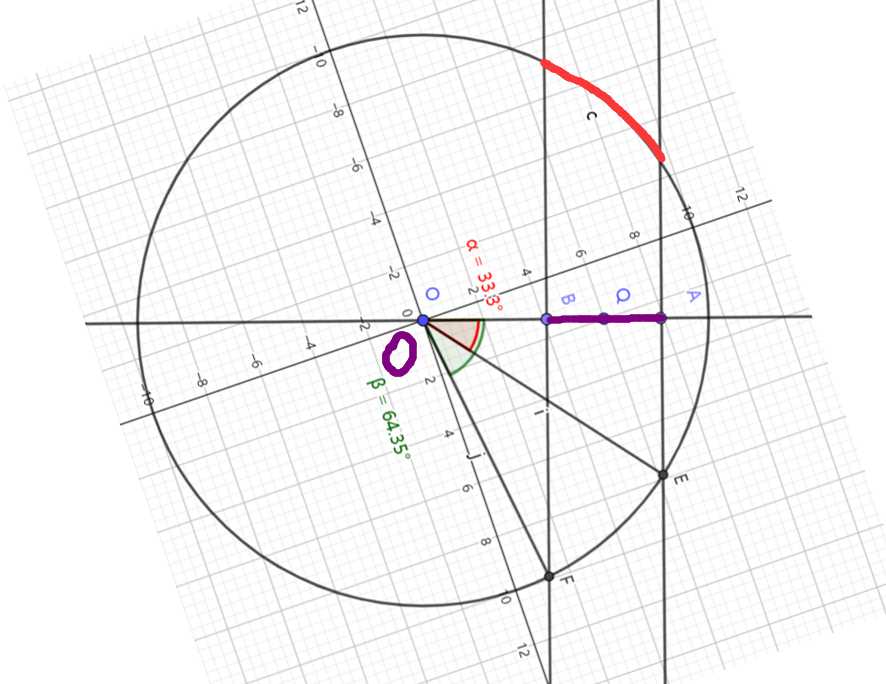
最后求出两个交点,然后用atan2算夹角theta
代码:
const double PI = acos(-1.0);
double calc(double x)
{
return sqrt(sqr(r)-sqr(x));
}
inline void Case_Test()
{
cin>>r>>x>>y>>d;
double p = sqrt(sqr(x)+sqr(y));//摆下来
double xl = p-d, xr = p+d;
double yl = calc(xl), yr = calc(xr);
double theta = atan2(yl,xl) - atan2(yr,xr);//这里我一开始还判断theta是否在[0,2PI)间。
cout<<fixed<<setprecision(11)<<theta*r<<endl;
}
I.Chiitoitsu(期望DP)
题意:给你麻将的13张牌,问你求小七对胡牌的期望回合数。每种牌最多不超过2张,一共34种牌,每种4张。
思路:第一次做期望DP。我一开始想的是如果我手上有单个1m,那么我再摸一个1m,那肯定需要留下来;那如果是摸到了个2m呢?我是需要留下打出2m还是打出手上的1m?
我们注意到现在外面的牌数一定是3个1m,3个1m,所以这两个属于一个性质,我选择打出2m。
总结一句话就是:最优策略是,若摸到的牌能够凑成一对,则丢弃单牌;否则就丢弃摸到的牌。
考虑DP求期望,令f[s][r]表示手中有s张单牌,且牌堆剩余r张就可以达成小七对的期望轮数。
- 若$s=1$则有 $f[s][r]=1+\frac{r-3}{r}f[s][r-1]$
- 若$s>1$则有 $f[s][r]=1+\frac{3s}{r}f[s-2][r-1]+\frac{r-3s}{r}f[s][r-1]$
也就是说我式子的1表示每一轮,新的一轮当然需要+1,第二种情况的$\frac{3s}{r}f[s-2][r-1]$表示的是从上一个状态抽中一个组成对子,多两个单牌的状态转移过来,因为我要是抽中一个组成对子,是可以解决两个单牌的(摸一个组成,打出一个)。那么另一个状态就是$\frac{r-3s}{r}f[s][r-1]$,也就是不选的结果,$s$没有变,从$r-1$摸一张转移过来。
预处理之后,直接读入,$O(1)$输出即可,时间复杂度为$O(7\times 136+T)$
代码:
int f[20][200];
inline void init()
{
for (int r=1;r<=123;r++)
{
int inv = qpow(r,mod-2,mod);//费马小定理 逆元的处理
for (int s=1;s<=13;s++)
{
if (r<s*3) continue;//负数当然不可取
if (s==1)
f[s][r] = (1 + (r-3)*inv%mod*f[s][r-1])%mod;
else
f[s][r] = (1 + 3*s*inv%mod*f[s-2][r-1]%mod
+ (r-3*s)*inv%mod*f[s][r-1]%mod)%mod;
}
}
}
inline void Case_Test()
{
map<string,int> mp;
cin>>s;
for (int i=0;i<26;i+=2)
{
string res="";
res += s[i];
res += s[i+1];
mp[res]++;
}
cnt = 0;
for (auto e:mp)
if (e.second%2)
cnt++;//单牌
cout<<f[cnt][123]<<endl;
}
J.Serval and Essay(拓扑排序)
这个题真的妙!
题意:给你一个有向图,你可以选择一个点感染它,让它感染连接该点的,点u感染的条件的是所有连接点u的点v都被感染了,u才会被感染,求选取一个点的最大感染数是多少?
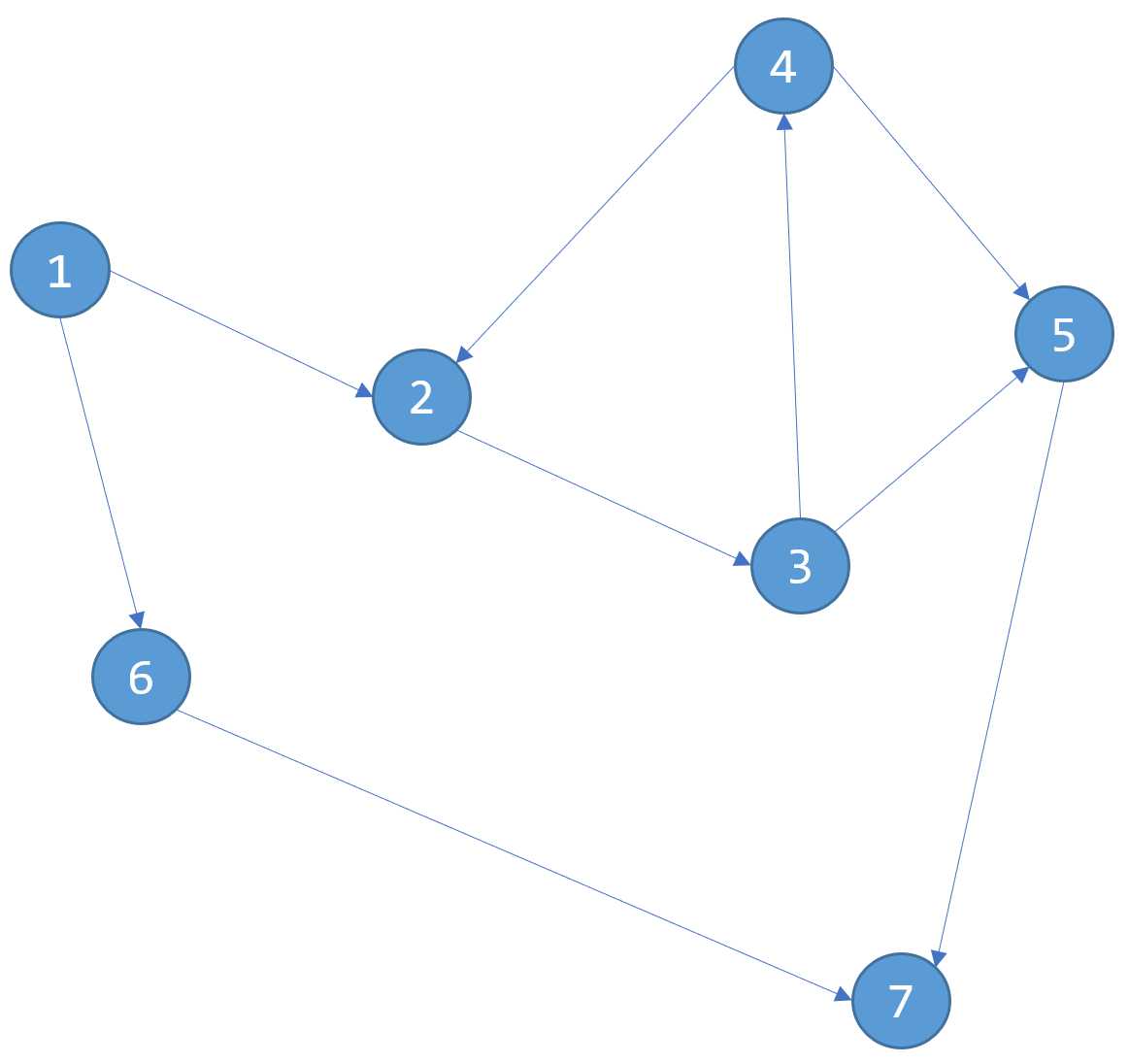
这个题从过题数来说应该算金牌题了吧,但是难度没有达到,补了!
思路:
- 1) 首先对每个点
u跑一次拓扑排序,如果在u的拓扑排序下面入栈的点v都标记,这些点不可能是最后的答案,因为如果选择v的话那么肯定不是最优的,而选择这个u肯定是最优的。因为有标记的存在,这个拓扑不会多,每个点最多访问两次。
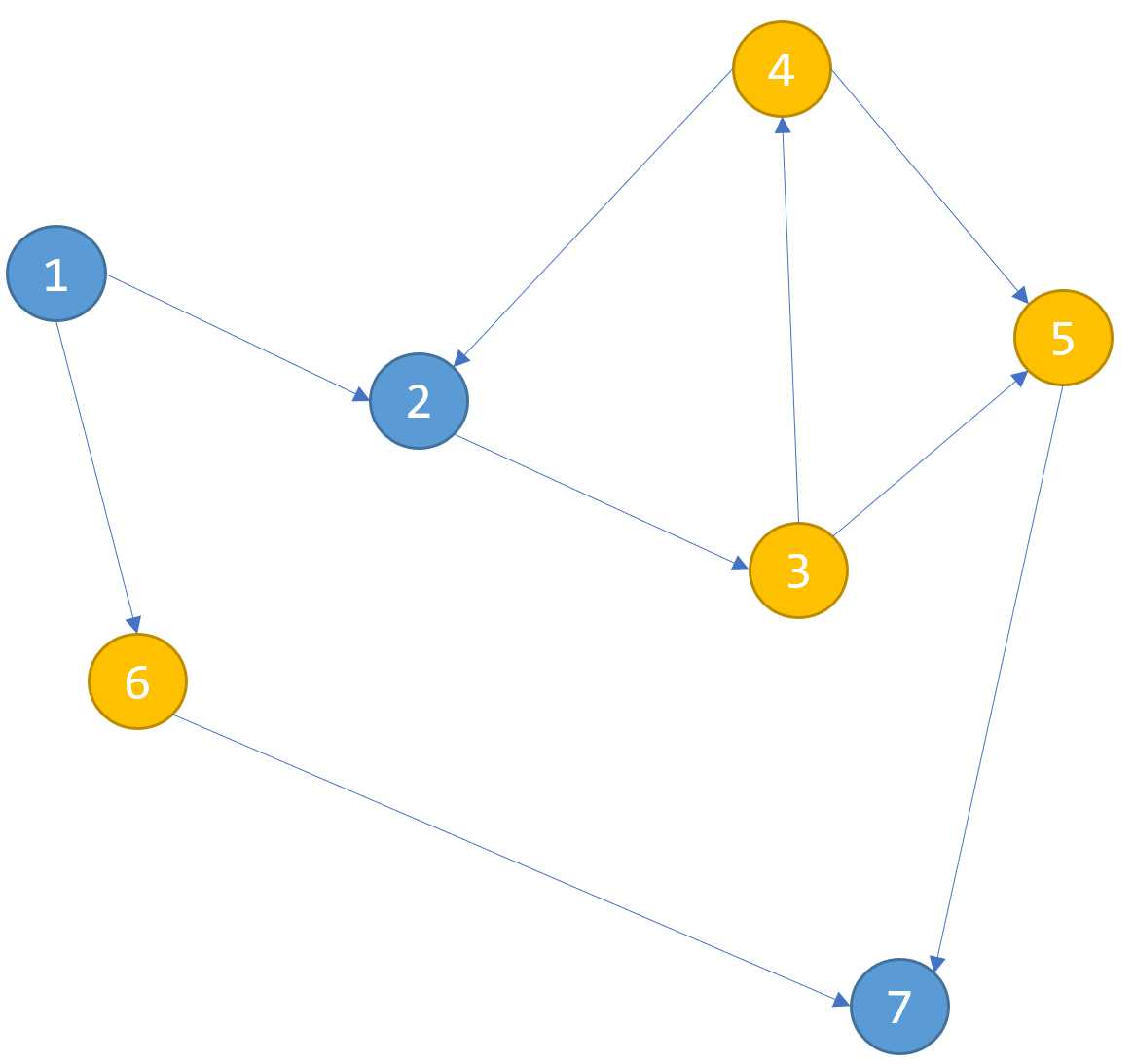
例如下图的,我们从顺序1..4去跑。

按顺序,1进入,对其能够拓展的点进行拓扑排序,这时候无法拓展,2进入,这时候发现能够达到的1是可以删除的,那么这时候标记1。

然后2无法拓展,按顺序轮到3,这时候可以拓展2,删除2...4进入也是同理,这样可以得到只有4没有被标记,1,2,3都被标记,表示的是这些点不可能成为最后的答案,因为我选择4肯定比这三个更优。

那如果是这样的1,2,3,4呢?

那么当1进入的时候,就可以把2,3,4全部排查掉,因为拓扑排序可以让他们全部进队列,注意:自己本身不要进,因为可能作为答案。
这样之后,我们可以发现样例只有三个点留下来了
for (int i=1;i<=n;i++)
{
if (!vis[i])//没有被标记,标记过肯定不用继续了
{
queue<int> q;
q.push(i);set<int> s;//set用来存改变了哪些in[],最后恢复
s.insert(i);
while (!q.empty())
{
x = q.front();q.pop();
for (int j=head[x];j;j=edge[j].next)
{
int y = edge[j].to;
if (y==i||vis[y]) continue;//一定要判vis[y],进入过不再进入,tle一发
in[y]--;//拓扑排序基操
s.insert(y);//标记修改过in[y]
if (in[y]==0)
{
q.push(y);
vis[y] = 1;
}
}
}
for (auto e:s)
in[e] = IN[e];//恢复原来的
}
}
- 2)然后对于所有可以遍历的点(
vis[i]==0)进行拓扑排序,因为这时候分成了若干块,所以不用考虑时间复杂度,所以每个点最多跑一次。也就是现在被分成了三种区域,
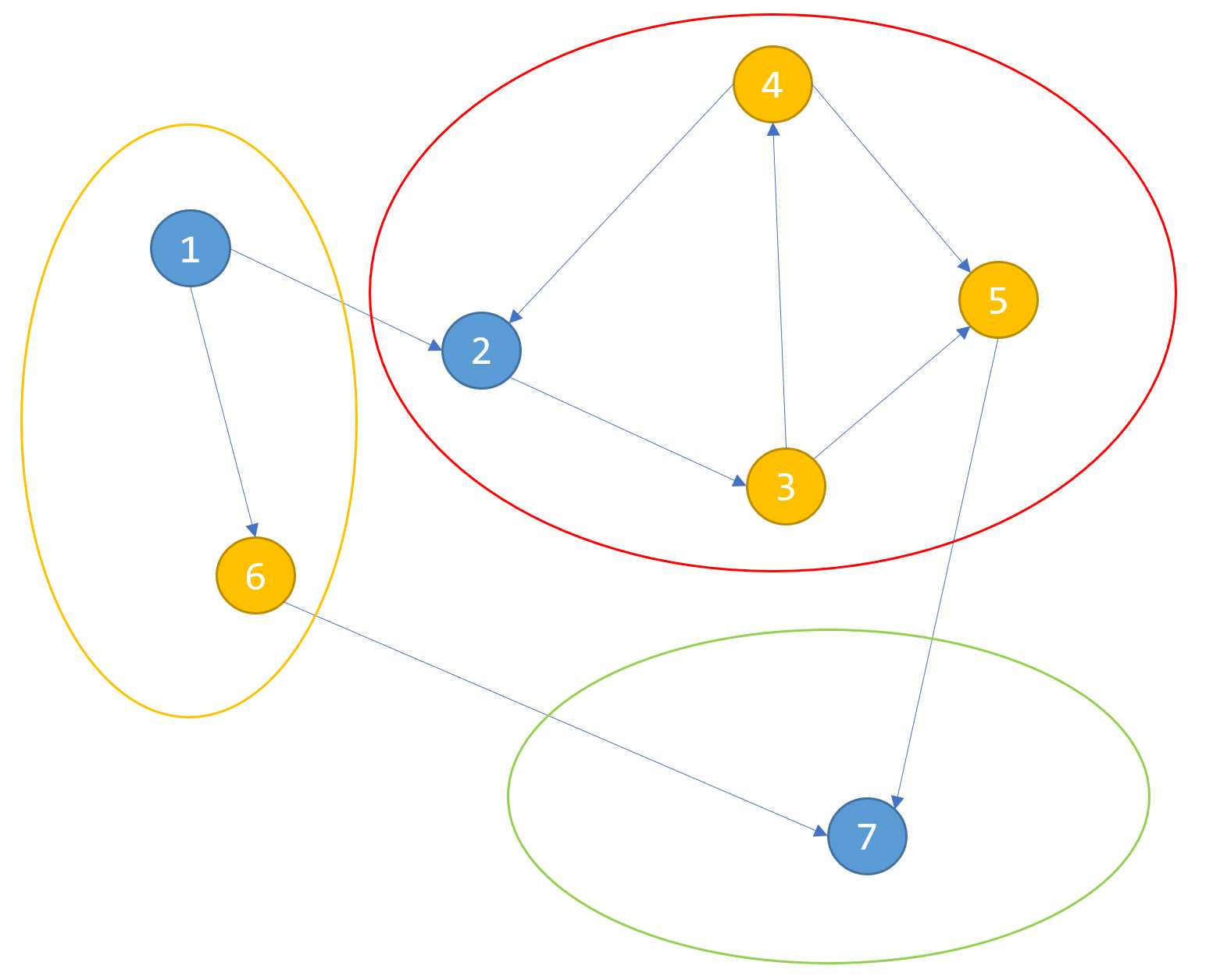
每个点最多一次,统计答案,ans每次取最大即可,注意记得恢复in[],不然当红色集合修改了7的入度的时候,这时候7是属于黄色集合的了(可以由6拓扑到)
ans = 1;
for (int i=1;i<=n;i++)
{
if (vis[i]) continue;
set<int> s;
queue<int> q;
s.insert(i);//一样的操作
q.push(i);
int res = 1;
while (!q.empty())
{
x = q.front();q.pop();
for (int j=head[x];j;j=edge[j].next)
{
int y = edge[j].to;
if (y==i) continue;//不用vis[y]是因为根本不会第二次进入了
in[y]--;
s.insert(y);
if (in[y]==0)
{
q.push(y);
res++;
}
}
}
for (auto e:s)
in[e] = IN[e];//恢复
ans = Max(ans,res);
}
代码:
inline void Case_Test()
{
cin>>n;
cnte = 0;
for (int i=1;i<=n;i++)
head[i] = 0, vis[i] = 0;
for (int i=1;i<=n;i++)
{
cin>>in[i];
IN[i] = in[i];
for (int j=1;j<=in[i];j++)
{
cin>>x;
add(x,i);
}
}
for (int i=1;i<=n;i++)
{
if (!vis[i])
{
queue<int> q;
q.push(i);set<int> s;
s.insert(i);
while (!q.empty())
{
x = q.front();q.pop();
for (int j=head[x];j;j=edge[j].next)
{
int y = edge[j].to;
if (y==i||vis[y]) continue;
in[y]--;
s.insert(y);
if (in[y]==0)
{
q.push(y);
vis[y] = 1;
}
}
}
for (auto e:s)
in[e] = IN[e];
}
}
ans = 1;
for (int i=1;i<=n;i++)
{
if (vis[i]) continue;
set<int> s;
queue<int> q;
s.insert(i);
q.push(i);
int res = 1;
while (!q.empty())
{
x = q.front();q.pop();
for (int j=head[x];j;j=edge[j].next)
{
int y = edge[j].to;
if (y==i) continue;
in[y]--;
s.insert(y);
if (in[y]==0)
{
q.push(y);
res++;
}
}
}
for (auto e:s)
in[e] = IN[e];
ans = Max(ans,res);
}
cout<<ans<<endl;
}
C.Grab the Seat!(贪心)
题意:给你一个二维坐标,在左侧有一块大屏幕从(0,1)到(0,m),然后在一个左下为(1,1)和右上为(n,m)的地方有电影院座位,现在有k个位置被占用,可以阻挡后面的人观看,有q组交换一个被占用的位置,每次交换后询问整场有多少个位置可以完完整整看到屏幕。
数据范围:$(2\leq n,m\leq 2\times 10^5,1\leq k\leq 2\times 10^5,1\leq q\leq 200)$
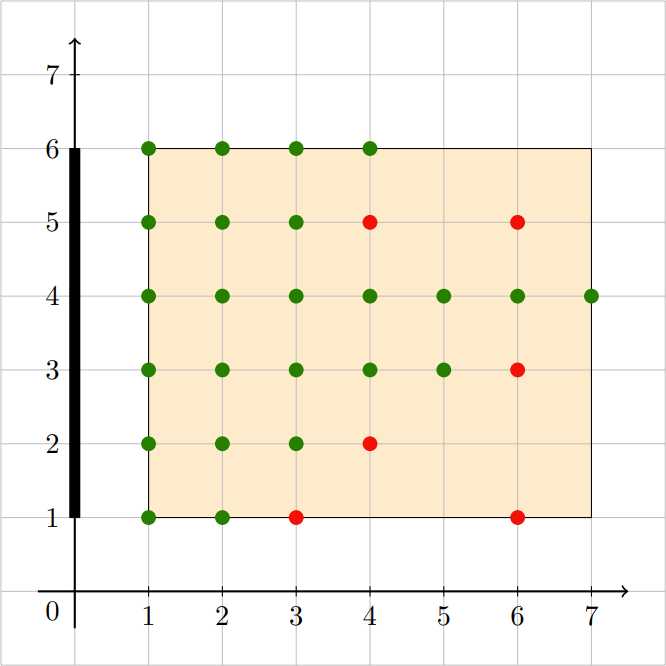
绿色的点表示可以观看完整的,红色表示占用的点
思路:先来好好看看,如果一个点被占用的影响是什么?
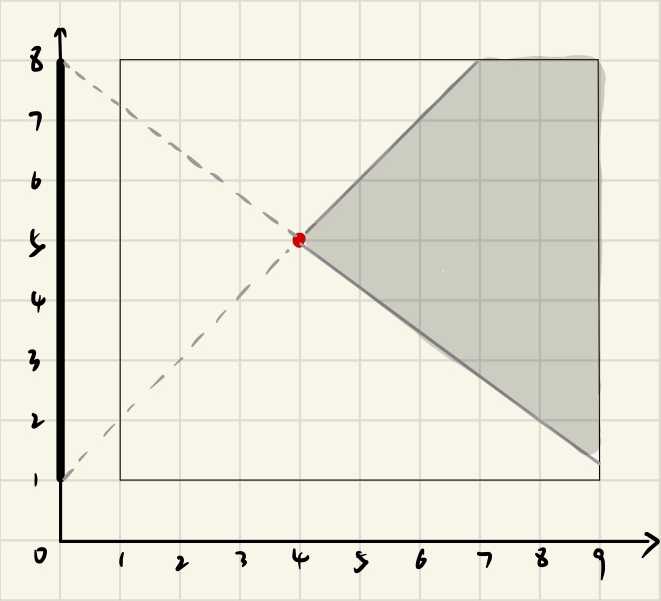
该点阻挡之后,连接(0,1)和(0,m)之后的所有区域都无法看见整块屏幕
如果这时候再来一个点:
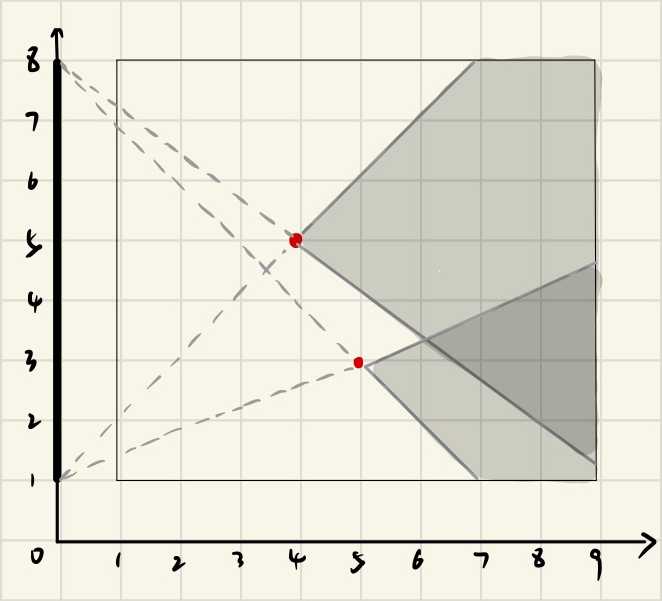
再多加一个点,则是这样的情况
那么如何维护?题解也给出了李超线段树的方法,我不会...我这里有一个贪心的做法。
从下往上和从上往下各扫一遍:
- 往上的时候每次维护
(0,1)与当前斜率最大(斜率最大印象最大)的点与当前第i行能够有多少人看到完整屏幕;(如下图橙色线) - 往下的时候每次维护
(0,m)与当前斜率最小(负数,越小越抖)的点与当前第i行能够有多少人能够看到完整屏幕。(如下图紫色线)
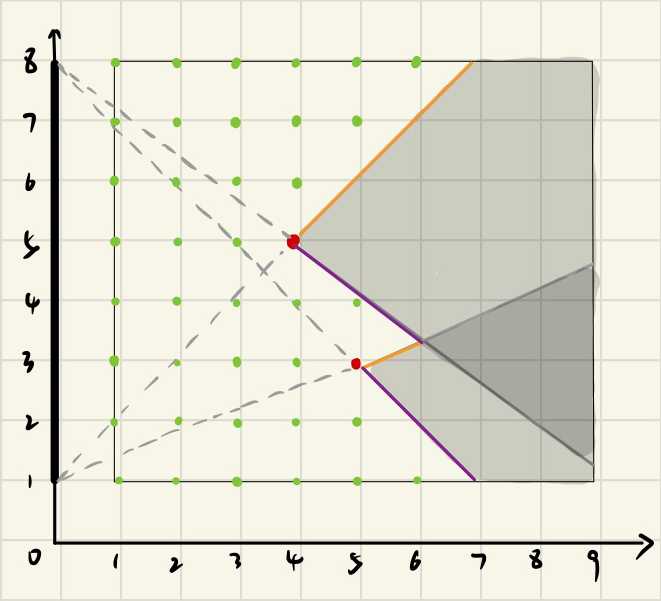
两个方向维护
例如来看从下往上的时候,遇到有点阻挡则判断如果当前的斜率大于原先的,则更新,用于计算接下来的能看到的点,例如下图i=4的时候我有x=5,y=3(斜率最大),我可以计算出当前直线方程当i=4时候计算出的点,这个点的左边都是可以看见的。
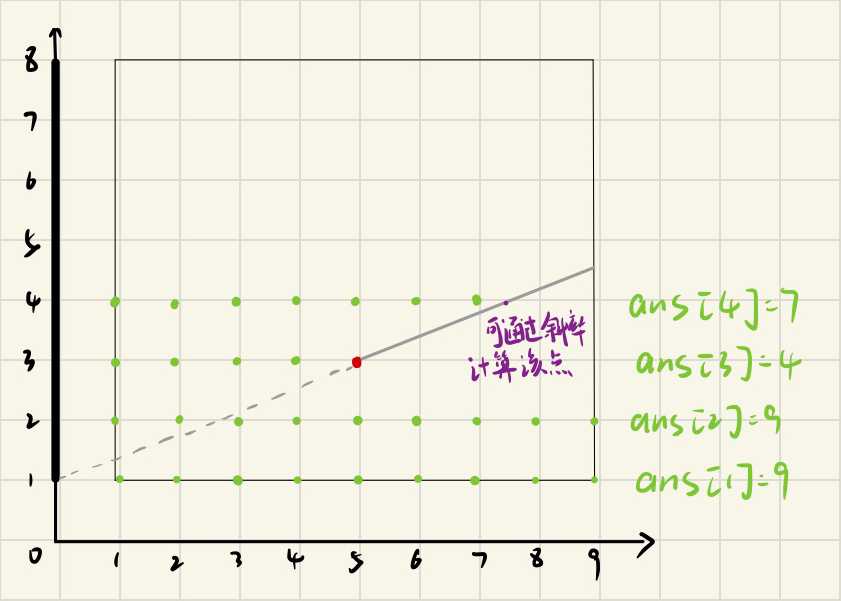
(5,3)的点会影响i=4的时候
按道理来说当i=1的时候,并不是所有的点都能看到,例如(9,1)这个点,是不是错了?不是,因为从上往下维护的时候就可以更新ans[1]。
接下来就是磨人的debug,首先需要考虑进入循环的时候x,y的设置,还有当上升且i=1下降且i=m的时候。
还有一个注意的就是,若(5,3)和(7,3)都有怎么办,我一开始选择sort一遍,每次取当前所需要的,就因为这个超时,然后就改成进入前先for一遍,更新ans[i],每次就不看点了,直接拿(ans[i],i)进行维护更新即可。
代码:
struct node
{
int x,y,id;
bool operator < (const node &rhs) const{
if (y==rhs.y) return x<rhs.x;
return y<rhs.y;
}
}a[N];
inline void Case_Test()
{
cin>>n>>m>>k>>q;
for (int i=1;i<=k;i++)
{
a[i].id = i;
cin>>a[i].x>>a[i].y;
}
while (q--)
{
cin>>p>>x>>y;
a[p].x = x;a[p].y = y;
for (int i=1;i<=m;i++)
ans[i] = n;
for (int i=1;i<=k;i++)
ans[ a[i].y ] = Min(ans[ a[i].y ] , a[i].x - 1);
x = inf,y = n+1;
for (int i=1;i<=m;i++)
{
int x0 = ans[i]+1, y0 = i;
if ( (y-1)*x0 < x*(y0-1) ) x = x0, y = y0;
if (y!=n+1&&y!=1) ans[i] = Min(ans[i] , ((i-1)*x+y-2)/(y-1)-1);
}
x = inf;y = n+1;
for (int i=m;i>=1;i--)
{
int x0 = ans[i]+1, y0 = i;
if ((y-m)*x0>(y0-m)*x) y = y0, x = x0;
if (y!=n+1&&y!=m) ans[i] = Min(ans[i] , ((i-m)*x+y-m+1)/(y-m)-1);
}
int sum = 0;
for (int i=1;i<=m;i++) sum += ans[i];
cout<<sum<<endl;
}
}

