比赛链接:Dashboard - Codeforces Round #806 (Div. 4) - Codeforces
div4因为昨天头晕,有些恍惚,感觉要猝死了,所以回去就早早躺床上玩手机到一点半才睡觉。今天晚上个人训练是昨天div4打了一场。
重点就是这个G题吧,其他的做一些小总结太简单了
A-F
A.YES or YES?
这里有个简便方法,就是如果是大写字母的话可以先用isupper(s[i])判断,然后用函数tolower(s[i])转化成小写。
B.ICPC Balloons
水题,我用set判断是否出现过,没出现就ans+=2,出现就ans++。
C.Cypher
简单,注意加一个大的10的倍数取模,我加10000然后对10取模的。
D.Double Strings
用map存,然后枚举长度(因为并不大),可以用substr函数来取出来,最后判断mp[s1],mp[s2]是否都存在即可。
string s1 = s.substr(0,p), s2 = s.substr(p);
- 注意:
这样s1得到的是前p个数,s2得到的是除了前p个数。
例如:s="carrynotkarry",然后s.substr(0,5)表示的是从0开始取5个数,也就是carry,然后s.substr(5)表示的是除去前5个,得到notkarry。
E.Mirror Grid
因为对称,$(i,j)$位置能够得到其他三个位置也就是:
$(j,n-i+1),(n-i+1,n-j+1),(n-j+1,i)$
F.Yet Another Problem About Pairs Satisfying an Inequality
送前往后扫一遍,满足条件对前面二分,然后再加入进去。
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
cin>>a[i];
ans = 0;
vector<int> v;
for (int i=1;i<=n;i++)
{
if (a[i]>=i) continue;
ans += lower_bound(v.begin(),v.end(),a[i])-v.begin();
v.emplace_back(i);
}
cout<<ans<<endl;
}
G.Good Key, Bad Key(贪心/DP)
题意
你有$n$个宝箱,每个宝箱有$a_i$个金币以及一个好钥匙代价$k$,你需要从前到后依次打开,你有两种钥匙去打开,分别是:
- 好钥匙。你可以得到当前$a_i$的所有金币,但是需要用$k$个金币的代价,允许赊账,也就是可以为负。
- 坏钥匙。你可以不用花费金币来打开,但是你需要让当前箱子以及后面的所有箱子减半,也就是$\left \lfloor \frac{a_i}{2} \right \rfloor ,\left \lfloor \frac{a_{i+1}}{2} \right \rfloor ,...,\left \lfloor \frac{a_n}{2} \right \rfloor $
PS:如果你再前一次已经使用了坏钥匙,后面再使用一次,则需要除以两次$2$。
求打开完所有箱子的最大金币数。
思路
这个题很有意思,首先需要证明一下:
用了一次坏钥匙之后,再也不可能用好钥匙来打开。
也就是好好好...好坏...坏坏坏
证明如下:
如果你在i的位置使用了坏钥匙,使得其与其下一个变成$\left \lfloor \frac{a_i}{2} \right \rfloor ,\left \lfloor \frac{a_{i+1}}{2} \right \rfloor$,这时候在使用了坏钥匙之后,第i+1个选择好钥匙打开,则代价为$\left \lfloor \frac{a_i}{2} \right \rfloor +\left \lfloor \frac{a_{i+1}}{2} \right \rfloor -k$。
但是我在i位置使用好钥匙,第i+1位置使用坏钥匙,我能得到的金币是 $a_i +\left \lfloor \frac{a_{i+1}}{2} \right \rfloor -k$,很明显:“好坏”是大于“坏好”的,所以能够得到箱子一定是好好好...好坏...坏坏坏
所以需要枚举分界线,哪里是好的最后一次,但是我对于坏每次都要计算a[i+1]/2以及a[i+1]/2/2以及...一直到n是否会超时?
不会。因为从数据来看最多除以32的$2$,所以最多枚举后面的$32$个数即可。时间复杂度当然就是$O(32n)$了。
思路都这样写了,我这里用f[i][j]来表示第i个箱子除以了j次2的金币个数。
for (int i=1;i<=n;i++)
{
cin>>f[i][0];
for (int j=1;j<=32;j++)
f[i][j] = f[i][j-1]/2;
}
例如第三个样例:
1
3 12
10 10 29
就会得到f[i][j]为:
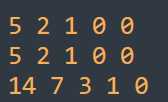
然后我用了前缀和...我一开始以为每个都要用前缀和,实际上只要存f[i][0]表示用好钥匙的前缀和即可...但是我对每一维都用了...继续看吧。
然后做前缀和
for (int j=0;j<=32;j++)
for (int i=1;i<=n;i++)
f[i][j]+=f[i-1][j];
现在f[i][j]变化成竖着的前缀和了,也就是下图:
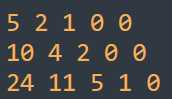
这样预处理之后,就对于“好坏”分开的地方进行枚举,枚举好的最后一个的位置
ans = 0;
for (int i=0;i<=n;i++)
{
int good = f[i][0]-f[0][0]-i*k;//前面i个,减去i个k的代价
int bad = 0;
for (int j=i+1,p=1;j<=n&&p<=32;j++,p++)
bad += f[j][p]-f[j-1][p];//每次减去下一个
ans = Max(ans,good+bad);//取max
}
cout<<ans<<endl;
最后输出即可。
(ps:不要纠结是32还是多少,够用就行)
代码
int f[N][33];
inline void Case_Test()
{
cin>>n>>k;
for (int i=1;i<=n;i++)
{
cin>>f[i][0];
for (int j=1;j<=32;j++)
f[i][j] = f[i][j-1]/2;
}
for (int j=0;j<=32;j++)
for (int i=1;i<=n;i++)
f[i][j]+=f[i-1][j];
ans = 0;
for (int i=0;i<=n;i++)
{
int good = f[i][0]-f[0][0]-i*k;//0..i good key
int bad = 0;
for (int j=i+1,p=1;j<=n&&p<=32;j++,p++)
bad += f[j][p]-f[j-1][p];
ans = Max(ans,good+bad);
}
cout<<ans<<endl;
}
