题意
题目链接:
2318 -- TOYS (poj.org)
2983. 玩具 - AcWing题库
约翰总是乱丢玩具,母亲给他准备了一个收纳盒,并且将收纳盒用若干的纸板分离开来,约翰每次会将玩具放在收纳盒中的一个地方,请问每一个收纳盒放了多少个玩具。收纳盒如下图:

给出$n,m,x_1,y_1,x_2,y_2$表示有$n$个纸板,$m$个玩具,有一个左上角坐标为$(x_1,y_1)$以及右下角坐标为$(x_2,y_2)$的收纳盒。
接下来$n$行每行有两个整数$U_i,L_i$表示第$i$个纸板的两端点坐标分别为$(U_i,y_1)$和$(L_i,y_2)$。保证纸板不相交并且从左至右顺序以此给出。
接下来$m$行,每行包括两个整数$X_j,Y_j$表示第$j$个玩具的坐标,给出的顺序是随机的,保证不会恰好落在纸板上,也不会再盒子外。
注意多组输入,以0结束。
输出需要输出每一个格子含有多少个玩具。x: y表示第x个盒子有y个,x从0开始。
数据范围
$1\leq n,m\leq 5000$
所有坐标在$[-10^5,10^5]$。
思路
这里最重要的是如何判断点属于哪个区域,我们可以把问题转化成点在线的左边还是右边,如果当前这个玩具在第$x$线的左边,那么也是在第$x+1$条线的左边,右侧的所有线也是如此,那么第$x-1$条以及左侧的所有线都在右边。

就如上图所示,一个玩具在线的左边还是右边是单调的——左左左...左右...右右右,注意这里需要手动将右边界填入,不然最后一个区域会出错。
所以为什么我用的是箭头而不是直线呢?(因为qq截图我没找到哪里是直线)因为我表示的是向量。
我这里的所有向量都是从下指向上面,那么问题来了,如何判断点在线的左边还是右边?
这里就要用到计算几何的知识了——叉积。
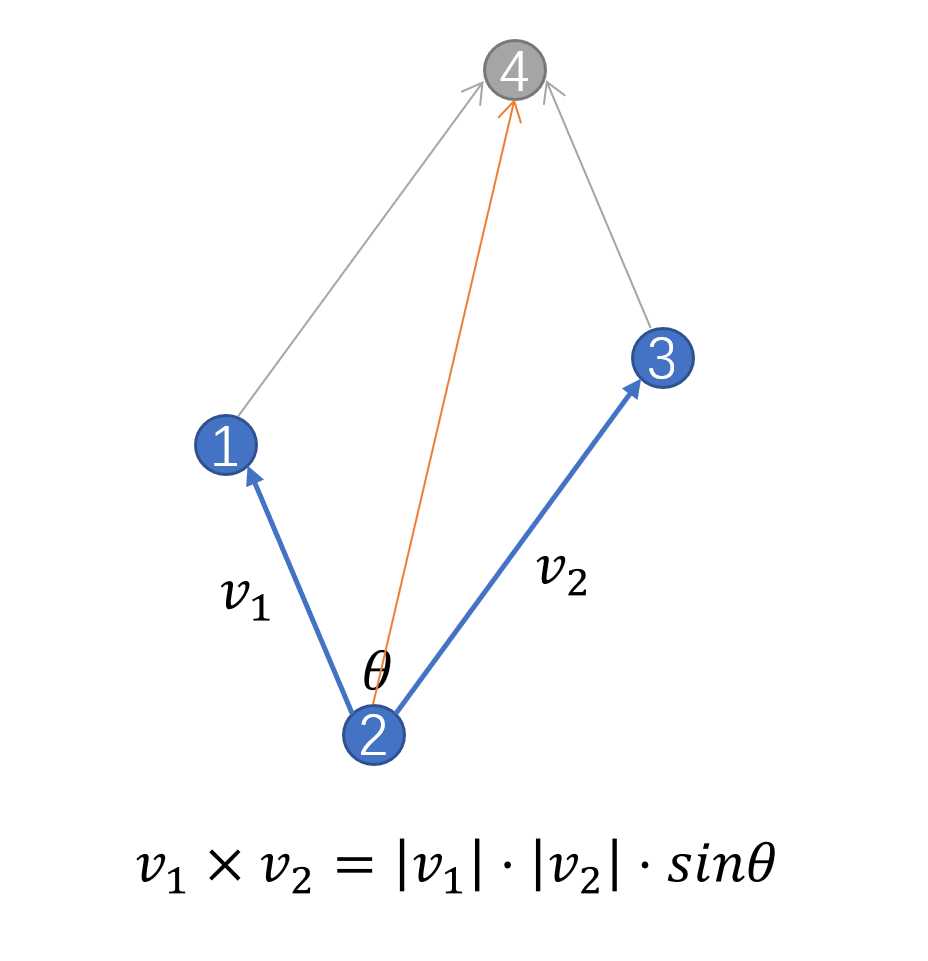
我们将该点与下边界的点形成一个向量,然后与隔板做叉积,注意顺序,因为$v_1\times v_2$与$v_2\times v_1$是不同的。因为叉积是有向的,如下图所示,左图就是负的,右图就是正的。
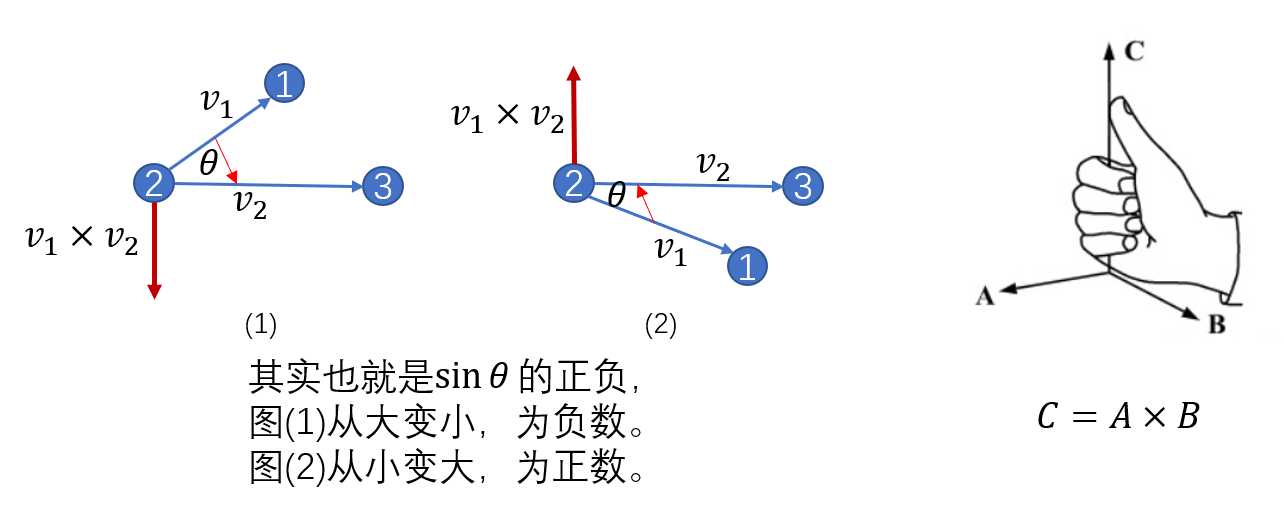
一共有$n$个玩具,每次比较需要$m$条板,还有若干组数据,所以时间复杂度肯定不够去$O(nm)$暴力查找,正因为有左左左...左右...右右右的单调,所以用到二分查找使得时间复杂度为$O(nlogm)$.
struct Point
{
double x,y;
Point(){}
Point(double _x,double _y):x(_x),y(_y){}
Point operator - (const Point &b)const{return Point(x-b.x,y-b.y);}
double operator ^ (const Point &b)const{return x*b.y-y*b.x;}//^为叉积
}a[N],b[N];
int ans[N];
double cross(Point a,Point b,Point c)
{
Point A(c-b),B(a-b);//按照顺序,c-b做v1,a-b做v2。然后A^B,a是上边界位置,b是下边界的位置
return A^B;
}
inline int find(double x,double y)
{
int l = 0, r = n;
while (l<r)
{
int mid = l+r>>1;
if (cross(a[mid],b[mid],Point(x,y))<0) r = mid;//二分
else l = mid+1;
}
return r;
}
最后对于每一次进入的判断即可。
代码
int n,m;
double x1,x2,y_1,y2,u,l;
int sgn(double x)
{
if (fabs(x)<eps) return 0;
return x>0?1:-1;
}
struct Point
{
double x,y;
Point(){}
Point(double _x,double _y):x(_x),y(_y){}
Point operator - (const Point &b)const{return Point(x-b.x,y-b.y);}
double operator ^ (const Point &b)const{return x*b.y-y*b.x;}
}a[N],b[N];
int ans[N];
double cross(Point a,Point b,Point c)
{
Point A(c-b),B(a-b);
return A^B;
}
inline int find(double x,double y)
{
int l = 0, r = n;
while (l<r)
{
int mid = l+r>>1;
if (cross(a[mid],b[mid],Point(x,y))<0) r = mid;
else l = mid+1;
}
return r;
}
inline void Case_Test()
{
bool ok = true;
while (cin>>n&&n)
{
cin>>m>>x1>>y_1>>x2>>y2;
for (int i=0;i<n;i++)
{
cin>>u>>l;
a[i] = {u,y_1};
b[i] = {l,y2};
}
a[n] = {x2,y_1};b[n] = {x2,y2};
for (int i=0;i<=n;i++) ans[i] = 0;
if (ok) ok=false;
else cout<<endl;
while (m--)
{
double x,y;
cin>>x>>y;
ans[find(x,y)]++;
}
for (int i=0;i<=n;i++)
cout<<i<<": "<<ans[i]<<endl;
}
}
