这个暑假跟着灵神(0x3f)做每日一题,一周的周一到周五下午三点是有每日一题的,大概是cf上面1700或者1800难度,这周因为最近力扣出一些dp题目,灵神在cf上也找了一些比较相似的写。在我之前的博客文章中也有很多出自灵神的每日一题里面。
CF166E. Tetrahedron (1500)
题意
题目链接:Problem - 166E - Codeforces
给你一个$n(1\leq n\leq 10^7)$,你一开始在顶点$D$上,你需要去走$n$步并且回到$D$点,求这样的方案数是多少(对mod取模)。
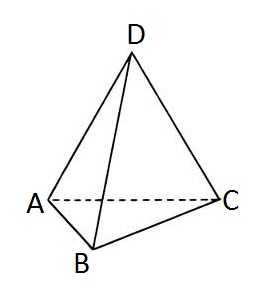
思路
这一看就是DP题,不难看出$A,B,C$点对于$D$点是对称的,贡献是一样的,也就是所以我定义:
dp[i][0]表示走i步到达$D$点的方案数dp[i][1]表示走i步到达$A/B/C$点的方案数
初始状态是dp[0][0] = 1,然后进行扫一遍,对于第i次:
- 首先看$D$ 点是可以由其他三点转移过来,所以
dp[i][0] = dp[i-1][1] * 3 % mod,乘以三是因为有三个点。 - 再来看$A/B/C$ 点是可以由$D$点转移过来(
dp[i-1][0]),也可以由其他两点转移过来(dp[i-1][1]*2)
代码
这个题比较简单
int dp[N][2];
inline void Case_Test()
{
cin>>n;
dp[0][0] = 1;
for (int i=1;i<=n;i++)
{
dp[i][0] = dp[i-1][1]*3%mod;
dp[i][1] = (dp[i-1][0] + dp[i-1][1]*2)%mod;
}
cout<<dp[n][0];
}
CF1105C. Ayoub and Lost Array (1500)
题意
题目链接:Problem - 1105C - Codeforces
给你一个正整数$n(1\leq n\leq 2\times 10^5$),还有$l,r(1\leq l\leq r\leq 10^9)$。求有多少个不同的长度为$n$的数组,数组元素值的范围为$[l,r]$,且数组元素之和为$3$的倍数。(对mod取模)
Input: 2 1 3
Output: 3
有三种可以符合的条件,分别是:$[1,2],[2,1],[3,3]$
思路
哪怕$l,r$的数再大,对我也没有关系,我只关心有多少个数对$3$取模为$1,2,0$,比如给你$l=2,r=8$,那么分成三类
- x[1]:对$3$取模为$1$的个数,$\lbrace 4,7\rbrace$。x[1] = 2
- x[2]:对$3$取模为$2$的个数,$\lbrace 2,5,8\rbrace$。x[2] = 3
- x[0]:对$3$取模为$0$的个数,$\lbrace 3,6\rbrace$。 x[0] = 2
我可以用一个二维数组来表示f[i][j]来表示选取了i个数后第j类($j=1,2,0$)有多少个。
我处理好这些之后来看怎么进行dp:
因为这里的每一个数字都是可以打乱顺序的,没有顺序要求,也可以重复,比如样例的$[1,2],[2,1]$是两种答案,所以相当于我每次选取i类都有x[i]种。
举个例子:假如第2类有$\lbrace 2,5,8 \rbrace$,我要选取$3$个有多少种情况呢?我只需要每次都乘以x[2]也就是$3^3=9$种,不难想象,分别是$[2,2,2],[2,2,5],[2,2,8],...,[8,8,5],[8,8,8]$
基于以上,可以来写递推式了:
对于f[i][0],可以从上一次0类再选一个0类,比在上一次的$3$的倍数那一类再选一个$3$的倍数进去。我也可以从上一次1类选一个2类进去,也就是在上一次对$3$取模为$1$的地方,选取一个对$3$取模为$2$的让其现在成为$3$的倍数。
其他情况都如此,也就是说对于一个f[i][j],我需要从上次的f[i-1][0],f[i-1][1],f[i-1][2]分别选出相应的类型让其变成j,其实也就是上一次的与选出的值相加对应j即可。
f[1][0] = x[0], f[1][1] = x[1], f[1][2] = x[2];
for (int i=2;i<=n;i++)
{
f[i][0] = (f[i-1][0]*x[0] + f[i-1][1]*x[2] + f[i-1][2]*x[1])%mod;
f[i][1] = (f[i-1][0]*x[1] + f[i-1][1]*x[0] + f[i-1][2]*x[2])%mod;
f[i][2] = (f[i-1][0]*x[2] + f[i-1][1]*x[1] + f[i-1][2]*x[0])%mod;
}
这样的时间复杂度是$O(n)$,这里值得一提的是,这个有$O(logn)$的时间复杂度的方法,也就是矩阵快速幂。
f = [x[0], x[1], x[2]]
x = [ [x[0], x[1], x[2]],
[x[2], x[0], x[1]],
[x[1], x[2], x[0]] ]
可以看出我由递推式可以的出这样的矩阵计算,乘以$n-1$次$x$矩阵。
代码
int l,r;
int f[N][3];
int x[3];
inline void Case_Test()
{
cin>>n>>l>>r;
m = r-l+1;
x[0] = x[1] = x[2] = m/3;
for (int i=l+(m/3)*3;i<=r;i++)
x[i%3]++;
f[1][0] = x[0], f[1][1] = x[1], f[1][2] = x[2];
for (int i=2;i<=n;i++)
{
f[i][0] = (f[i-1][0]*x[0] + f[i-1][1]*x[2] + f[i-1][2]*x[1])%mod;
f[i][1] = (f[i-1][0]*x[1] + f[i-1][1]*x[0] + f[i-1][2]*x[2])%mod;
f[i][2] = (f[i-1][0]*x[2] + f[i-1][1]*x[1] + f[i-1][2]*x[0])%mod;
}
cout<<f[n][0];
}
/*可以用矩阵快速幂加速
f = [x[0], x[1], x[2]]
x = [ [x[0], x[1], x[2]],
[x[2], x[0], x[1]],
[x[1], x[2], x[0]] ]
qpow(n-1)次
*/
CF788A. Functions again (1600)
题意
题目链接:Problem - 788A - Codeforces
给你一个长度为$n(1\leq n\leq 10^5)$的数组$a(-10^9\leq a_i\leq 10^9)$,在满足$1\leq l<r\leq n$的前提下,输出$f(l,r)$的最大值,$f$的定义如下:
$$
f(l,r)=\sum_{i=1}^{r-1}|a[i]-a[i+1]|\cdot (-i)^{i-l}
$$
思路
- 对于奇偶性相同的$l$,$(-1)^{i-l}$的变化规律是相同的,也就是$+,-,+,-,...$。所以需要进行分开讨论。
-
其实求得就是$|a[i]-a[i+1]|\cdot (-1)^{i-l}$的最大子段和(贪心扫一遍去找)
-
正如第一条所说,只需要从对于奇偶性不同的来说,从$1$开始一遍,再从$2$开始一遍取
Max即可。
代码
inline void Case_Test()
{
cin>>n;
for (int i=1;i<=n;i++)
cin>>a[i];
int flag = 1;//flag每次变化1,-1,1,-1,...
int sum = 0;
for (int i=1;i<n;i++)
{
if (i%2==1 && sum<0)
sum = 0;
sum += flag*Abs(a[i]-a[i+1]);
flag *= -1;
ans = Max(ans, sum);
}
flag = 1;
sum = 0;
for (int i=2;i<n;i++)//从2开始再来一遍
{
if (i%2==0 && sum<0)
sum = 0;
sum += flag*Abs(a[i]-a[i+1]);
flag *= -1;
ans = Max(ans, sum);
}
cout<<ans;
}
CF1084C. The Fair Nut and String (1500)
题意
题目连接:Problem - 1084C - Codeforces
给你一个字符串$s$,长度不超过$10^5$,只有小写字母组成。求出满足如下条件$s$下标序列的$p$的个数
- 对于每一个$i$,都有$s_{p_i}='a'$
- 满足从小到大的关系$p_i<p_{i+1}$
- 相邻两个序列下标之间需要至少有一个
'b',也就是$s_{p_i}$和$s_{p_{i+1}}$之间。
思路
用f[i]表示s的前i个字母的合法序列个数。
- 当s[i]!='a'时候,就继承f[i]=f[i-1]
- 当s[i]=='a'的时候,f[i]=f[i-1]+f[last['b']]+1,这里的$1$表示新加自己,然后last['b']表示的是上一次b出现的下标。
答案就是f[n]了。
至于第二个式子怎么来的,可以这么理解:第一个f[i-1]表示不选,f[last['b']表示选择当前的,当前的不与前一个字母有关,而是与前一个b有关。
代码
vector<int> v;
int f[N];
inline void Case_Test()
{
cin>>s;
n = s.length();
s = " " + s;
v.push_back(0);
for (int i=1;i<=n;i++)
if (s[i]=='b') v.push_back(i);
v.push_back(n+1);
x = 0;
for (int i=1;i<=n;i++)
{
if (s[i]=='a')
f[i] = (f[i-1] + f[v[x]] + 1) %mod;
else
{
if (s[i]=='b')
x++;
f[i] = f[i-1];
}
}
cout<<f[n];
}
这里的v和x是找上一个b出现的位置。
也可以简化成一维的
inline void Case_Test()
{
cin>>s;
n = s.size();
for (int i=0;i<n;i++)
if (s[i]=='a')
ans = (ans + pre + 1) % mod;
else if (s[i]=='b')
pre = ans;
cout<<ans;
}
至此,灵神这周的每日一题就写在这里的。下周继续!
