题目
题目来源于大连大学2022年4月程序设计竞赛,我和伍老师合砍12题rk23,差两题ak。
题目链接:F-旅行_大连大学2022年4月程序设计竞赛(同步赛) (nowcoder.com)

一句话题意:给你n点m边的有向图,每条边有边权,点没有点权,q次询问,每次询问点x是否在点1到点n的最短路径上,最短路径可能有多条。
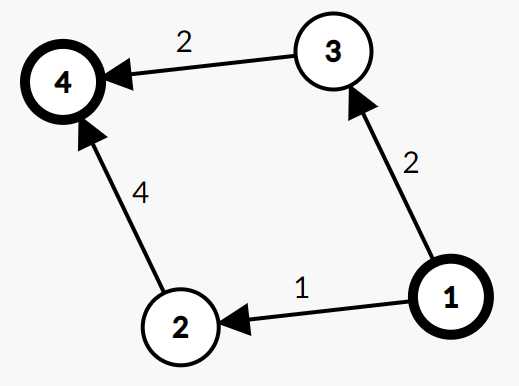
如上图,从1到4的话,最短路当然是"1->3->4",这三个点都是,而2不是。
思路
我们先用一个二维数组dis[i][j]来表示点i到点j之间的最短距离,那么对于起点是1,终点是n来说,询问一个点x是不是在1到n的最短路径上,我们有这样的结论:
如果满足1到x的最短距离加上x到n的最短距离等于1到n的最短距离,即:dis[1][x] + dis[x][n] == dis[1][n]。
分析一下:
1)dis[1][x] + dis[x][n] < dis[1][n]怎么办?答案是不会发生的,因为如果小的话,那么dis[1][n]的最短距离肯定不是这个了,而是dis[1][x] + dis[x][n],会更新dis。
2)dis[1][x] + dis[x][n] == dis[1][n]。这个时候就是在最短路径上,因为我松弛操作的时候也是这样而来的
3)dis[1][x] + dis[x][n] > dis[1][n]。这个时候的话,说明x不在最短路径上,因为我有别的路能比"1->...->x->...->n"更短,不会经过x。
接下来一个问题,用二维数组去Floyd时间复杂度显然不现实,但是对于Dijkstra这个单元最短路来说,我们只能求出点s到其他所有点的最短距离。所以我们想到——反向建图
这个时候我们用终点n作为Dijkstra的起点进行跑图,这样求出来的dis1[i]表示的是反向图中从点n到点i的最短距离,因为是有向图且是反向建边,所以这个距离也表示正向图中从点i到点n的最短距离。
代码
struct node
{
int to,next,w;
}edge[N<<1],edge1[N<<1];
int head[N],cnt,n,m,x,y,w,s,t,dis[N];
bool exist[N];
inline void add(int x,int to,int w)
{
edge[++cnt].to=to;
edge[cnt].next=head[x];
edge[cnt].w=w;
head[x]=cnt;
}
inline void Dij(int s,int t)
{
memset(dis,0x7f/2,sizeof(dis));
mem(exist,0);
dis[s]=0;
priority_queue<pair<int,int> > Q;
Q.push({0,s});
while (!Q.empty())
{
int x=Q.top().second;Q.pop();
if (exist[x]) continue;
exist[x]=true;
for (int i=head[x];i;i=edge[i].next)
{
int y=edge[i].to,w=edge[i].w;
if (dis[y]>dis[x]+w)
{
dis[y]=dis[x]+w;
Q.push({-dis[y],y});
}
}
}
//cout<<dis[t];
}
//反向建图
int head1[N],cnt1,dis1[N];
inline void add1(int x,int to,int w)
{
edge1[++cnt1].to=to;
edge1[cnt1].next=head1[x];
edge1[cnt1].w=w;
head1[x]=cnt;
}
inline void Dij1(int s,int t)
{
memset(dis1,0x7f/2,sizeof(dis1));
mem(exist,0);
dis1[s]=0;
priority_queue<pair<int,int> > Q;
Q.push({0,s});
while (!Q.empty())
{
int x=Q.top().second;Q.pop();
if (exist[x]) continue;
exist[x]=true;
for (int i=head1[x];i;i=edge1[i].next)
{
int y=edge1[i].to,w=edge1[i].w;
if (dis1[y]>dis1[x]+w)
{
dis1[y]=dis1[x]+w;
Q.push({-dis1[y],y});
}
}
}
//cout<<dis[t];
}
inline void Case_Test()
{
int q;
cin>>n>>m>>q;
for (int i=1;i<=m;i++)
{
cin>>x>>y>>w;
add(x,y,w);
add1(y,x,w);
}
Dij(1,n);Dij1(n,1);//正反都跑一次,起点和重点反过来
while (q--)
{
cin>>x;
if (dis[x]+dis1[x]==dis[n]) cout<<"yes"<<endl;//上文分析的
else cout<<"no"<<endl;
}
}
